中国地质调查局主办
高级检索

河北坝上高原如意河流域风积沙厚度空间展布预测方法

,  ,  ,  ,  , 

文章导航 > 地质通报 > 2022 > 41(12): 2138-2145

上一篇

下一篇

邵海, 殷志强, 王轶, 邢博, 彭令, 王瑞丰. 河北坝上高原如意河流域风积沙厚度空间展布预测方法[J]. 地质通报, 2022, 41(12): 2138-2145. doi: 10.12097/j.issn.1671-2552.2022.12.006
引用本文: 邵海, 殷志强, 王轶, 邢博, 彭令, 王瑞丰. 河北坝上高原如意河流域风积沙厚度空间展布预测方法[J]. 地质通报, 2022, 41(12): 2138-2145. doi: 10.12097/j.issn.1671-2552.2022.12.006
shu
SHAO Hai, YIN Zhiqiang, WANG Yi, XING Bo, PENG Ling, WANG Ruifeng. Prediction methods of spatial distribution of aeolian sand in Ruyi River Basin of Bashang Plateau, Hebei Province[J]. Geological Bulletin of China, 2022, 41(12): 2138-2145. doi: 10.12097/j.issn.1671-2552.2022.12.006
Citation: SHAO Hai, YIN Zhiqiang, WANG Yi, XING Bo, PENG Ling, WANG Ruifeng. Prediction methods of spatial distribution of aeolian sand in Ruyi River Basin of Bashang Plateau, Hebei Province[J]. Geological Bulletin of China, 2022, 41(12): 2138-2145. doi: 10.12097/j.issn.1671-2552.2022.12.006
shu

河北坝上高原如意河流域风积沙厚度空间展布预测方法

  • 1.

    中国地质环境监测院, 北京 100081

  • 2.

    中国地质调查局自然资源综合调查指挥中心, 北京 100055

  • 3.

    地质灾害防治与地质环境保护国家重点实验室(成都理工大学), 四川 成都 610059

  • 4.

    河北省山区地质环境重点实验室, 河北 承德 067000

  • 基金项目:
    中国地质环境监测院研发基金项目《地表基质中的土壤层厚度空间分布预测模型研究——以坝上高原如意河流域为例》(编号: 20220107)、国家自然科学基金项目《构造差异隆升影响下顺构造地貌发育强度对大型滑坡的控制机理和孕灾模式——以美姑河流域为例》(批准号: 41977258)、中国地质调查局项目《全国自然资源监测评价与智慧服务》(编号: DD20221761)和河北省重点研发计划项目《京津冀水源涵养区坝上生态环境脆弱带修复模式与立体监测技术综合研究》(编号: 20374207D)
详细信息
    作者简介: 邵海(1986-), 男, 在读博士生, 高级工程师, 从事地表基质与工程地质调查研究。E-mail: shaohai@mail.cgs.gov.cn
    通讯作者: 殷志强(1980-), 男, 博士, 正高级工程师, 从事第四纪地质环境演化与地表基质研究。E-mail: yinzhiqiang@mail.cgs.gov.cn

  • 中图分类号: P62

Prediction methods of spatial distribution of aeolian sand in Ruyi River Basin of Bashang Plateau, Hebei Province

  • 1.

    China Institute of Geo-Environment Monitoring, Beijing 100081, China

  • 2.

    Natural Resources Comprehensive Survey Command Center, China Geological Survey, Beijing 100055, China

  • 3.

    State Key Laboratory of Geohazard Prevention and Geoenvironment Protection(Chengdu University of Technology), Chengdu 610059, Sichuan, China

  • 4.

    Hebei Key Laboratory of Mountain Geological Environment, Chengde 067000, Heibei, China

More Information

    摘要

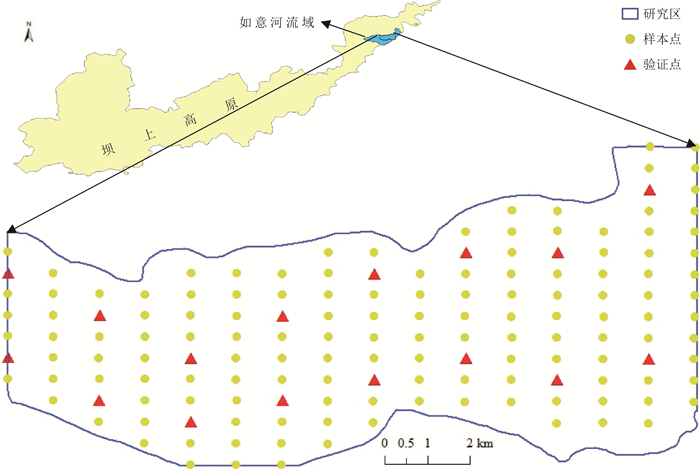
  • 不同的空间插值方法会对风积沙厚度空间分布预测精度产生重要影响。基于河北承德坝上高原东部如意河流域中游152组风积沙厚度数据，应用径向基函数人工神经网络(RBF-ANN)插值方法探究如意河流域中游风积沙厚度空间分布特征，并与地统计插值方法中的不同模型函数、确定性插值中的不同插值方法进行预测误差和计算结果对比分析。结果表明，在地统计插值方法中，经典贝叶斯克里金插值-幂半变异函数(EBK- Power)的插值效果最佳；在确定性插值方法中，径向基函数(RBF)插值效果最佳；RBF-ANN插值较EBK- Power和RBF方法在平均绝对误差(MAE)上的改进大于30%，在均方根误差(RMSE)上的改进大于20%，RBF-ANN插值更适用于如意河流域风积沙厚度空间分布预测。

    Different spatial interpolation methods will have an important influence on the prediction accuracy of the spatial distribution of aeolian sand thickness.Based on the data of 152 groups of aeolian sand thickness in the middle reaches of Ruyi River Basin in the east of Bashang Plateau, Chengde, this paper used the Radial Basis Function-Artificial Neural Network(RBF-ANN)interpolation method to explore the spatial distribution characteristics of aeolian sand thickness in this area, and compared the prediction error and calculation results among different model functions in geostatistical analyst method and different interpolation methods in deterministic interpolation method.The results showed that among the geostatistical analyst methods, the classical EBK-Power has the best interpolation effect and among the deterministic interpolation methods the RBF interpolation is the best.Compared with EBK-Power and RBF interpolation, RBF-ANN interpolation improves the mean absolute error by more than 30%, and the improvement on the root mean square error was more than 20%, so it was concluded that RBF-ANN interpolation was more suitable for predicting the spatial distribution of aeolian sand thickness in Ruyi River Basin.

    • HTML全文
  • 加载中

  • 图 1  如意河流域中游风积沙厚度调查点空间分布

    Figure 1. 

    下载: 全尺寸图片 幻灯片

    图 2  不同地统计插值方法的风积沙厚度空间分布

    Figure 2. 

    下载: 全尺寸图片 幻灯片

    图 3  不同确定性插值方法和RBF-ANN插值方法的风积沙厚度空间分布

    Figure 3. 

    下载: 全尺寸图片 幻灯片

    表 1  如意河流域中游风积沙厚度统计特征值

    Table 1.  Statistical characteristic value of aeolian sand thickness in the middle reaches of Ruyi River Basin

    项目 样本个数 最大值/m 最小值/m 平均值/m 偏度 峰度 标准差/m 变异系数
    样本数据集 136 12.00 0 2.66 1.37 1.95 2.45 0.92
    验证数据集 16 8.00 0 2.38 1.25 1.41 2.19 0.92
    下载: 导出CSV

    表 2  风积沙厚度的地统计插值方法预测精度

    Table 2.  Prediction accuracy analysis of geostatistical interpolation method for aeolian sand thickness

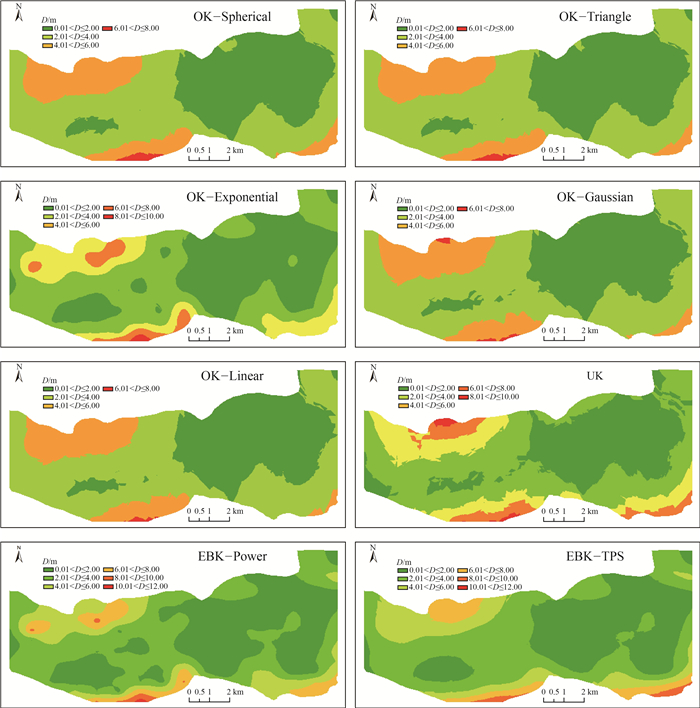
    数据集类型 插值方法 模型函数类型 MAE RMSE RMSSE
    样本数据集 普通克里金(OK) 球面函数(Spherical) 0.0475 1.47 1.1652
    三角函数(Triangle) 0.0551 1.52 1.1649
    指数函数(Exponential) 0.0121 0.77 1.0812
    高斯函数(Gaussian) 0.0556 1.76 1.1650
    线性函数(Linear) 0.0749 1.62 1.1648
    泛克里金(UK) 与一次漂移函数成线性关系(LLD) 0.1840 1.72 1.0814
    经典贝叶斯克里金(EBK) 幂半变异函数(Power) 0.0036 0.26 0.9706
    薄板样条半变异函数(TPS) 0.0716 1.18 0.9512
    验证数据集 普通克里金(OK) 球面函数(Spherical) 0.0254 1.74
    三角函数(Triangle) 0.0254 1.75
    指数函数(Exponential) 0.0405 1.68
    高斯函数(Gaussian) 0.0308 1.77
    线性函数(Linear) 0.0250 1.78
    泛克里金(UK) 与一次漂移函数成线性关系(LLD) 0.0766 1.71
    经典贝叶斯克里金(EBK) 幂半变异函数(Power) 0.0956 1.58
    薄板样条半变异函数(TPS) 0.0687 1.57
    下载: 导出CSV

    表 3  风积沙厚度的地统计插值方法预测结果

    Table 3.  Prediction result analysis of geostatistical interpolation method for aeolian sand thickness

    插值方法 模型函数类型 最大值/m 最小值/m 平均值/m 标准差/m
    普通克里金(OK) 球面函数(Spherical) 7.32 0.24 2.63 1.35
    三角函数(Triangle) 7.08 0.24 2.62 1.33
    指数函数(Exponential) 9.96 0.14 2.65 1.60
    高斯函数(Gaussian) 6.30 0.25 2.63 1.29
    线性函数(Linear) 6.59 0.24 2.60 1.28
    泛克里金(UK) 与一次漂移函数成线性关系(LLD) 9.34 0.24 2.91 1.66
    经典贝叶斯克里金(EBK) 幂半变异函数(Power) 11.41 0.05 3.12 1.79
    薄板样条半变异函数(TPS) 10.03 0.08 2.81 1.83
    下载: 导出CSV

    表 4  风积沙厚度的确定性插值方法预测精度

    Table 4.  Prediction accuracy analysis of deterministic interpolation method for aeolian sand thickness

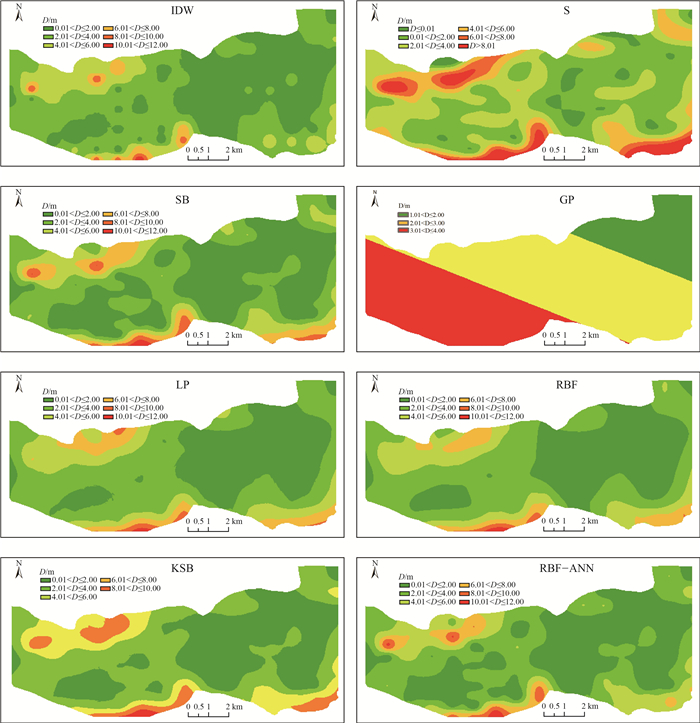
    插值方法 样本数据集 验证数据集
    MAE RMSE MAE RMSE
    反距离权重(IDW) 0.0003 0.08 0.0252 1.72
    样条函数(S) 0.0055 0.04 0.0528 1.97
    含障碍的样条函数(SB) 0 0 0.1514 1.79
    全局多项式插值(GP) 0.0048 2.34 0.4271 2.21
    局部多项式插值(LP) 0.1281 0.94 0.0162 1.68
    径向基函数插值(RBF) 0.0036 0.03 0.0228 1.61
    含障碍的核插值(KSB) 0.1362 1.17 0.0081 1.62
    下载: 导出CSV

    表 5  风积沙厚度的确定性插值方法预测结果

    Table 5.  Prediction result analysis of deterministic interpolation method for aeolian sand thickness

    插值方法 最大值/m 最小值/m 平均值/m 标准差/m
    反距离权重(IDW) 11.41 0.05 3.12 1.79
    样条函数(S) 17.58 -6.41 2.70 2.52
    含障碍的样条函数(SB) 11.41 0.05 3.12 1.79
    全局多项式插值(GP) 3.88 1.00 2.69 0.65
    局部多项式插值(LP) 11.41 0.05 3.12 1.79
    径向基函数插值(RBF) 11.41 0.05 3.12 1.79
    含障碍的核插值(KSB) 11.41 0.05 3.12 1.79
    下载: 导出CSV

    表 6  风积沙厚度的不同插值方法预测精度分析

    Table 6.  Analysis of prediction accuracy of aeolian sand thickness by different interpolation methods

    插值方法 样本数据集 验证数据集
    MAE RMSE MAE RMSE
    经典贝叶斯克里金-幂半变异函数
    (EBK-Power)    		 0.0036 0.26 0.0687 1.67
    径向基函数插值(RBF) 0.0036 0.03 0.0228 1.61
    径向基函数人工神经网络(RBF-ANN) 0.0025 0.02 0.0170 1.28
    下载: 导出CSV
    • 参考文献(24)
  • [1]

    殷志强, 秦小光, 张蜀冀, 等. 地表基质分类及调查初步研究[J]. 水文地质工程地质, 2020, 47(6): 14-20. https://www.cnki.com.cn/Article/CJFDTOTAL-SWDG202006003.htm

    [2]

    何煦, 桑琦明, 郑粉莉, 等. 东北不同黑土厚度区多营力作用的坡面土壤侵蚀试验研究[J]. 水土保持学报, 2021, 35(1): 103-109, 115. https://www.cnki.com.cn/Article/CJFDTOTAL-TRQS202101015.htm

    [3]

    张珍明, 周运超, 黄先飞, 等. 喀斯特小流域土壤有机碳密度空间异质性及影响因素[J]. 自然资源学报, 2018, 33(2): 313-324. https://www.cnki.com.cn/Article/CJFDTOTAL-ZRZX201802011.htm

    [4]

    易湘生, 李国胜, 尹衍雨, 等. 土壤厚度的空间插值方法比较—以青海三江源地区为例[J]. 地理研究, 2012, 31(10): 1793-1805. https://www.cnki.com.cn/Article/CJFDTOTAL-DLYJ201210006.htm

    [5]

    金保明, 林鹏, 李光敦. 基于运动波壤中流理论与无限边坡稳定分析理论的滑坡预测模型[J]. 工程科学与技术, 2021, 53(4): 140-148. https://www.cnki.com.cn/Article/CJFDTOTAL-SCLH202104015.htm

    [6]

    王占亮, 卫晓锋, 魏浩, 等. 河北坝上小滦河流域不同沉积单元粒度特征及其荒漠化的影响[J]. 矿产勘查, 2021, 12(4): 1000-1007. https://www.cnki.com.cn/Article/CJFDTOTAL-YSJS202104029.htm

    [7]

    安永龙, 黄勇, 张艳玲, 等. 北京房山南部地区富硒土壤生物有效性特征及来源[J]. 地质通报, 2020, 39(2/3): 387-399. http://dzhtb.cgs.cn/gbc/ch/reader/view_abstract.aspx?file_no=2020020319&flag=1

    [8]

    Liu J, Chen X, Lin H, et al. A simple geomorphic-based analytical model for predicting the spatial distribution of soil thickness in headwater hillslopes and catchments[J]. Water Resources Research, 2013, 49(11): 7733-7746.

    [9]

    Peníek V, Borvka L. Soil depth prediction supported by primary terrain attributes: A comparison of methods[J]. Plant Soid and Enviroment, 2006, 52: 424-430.

    [10]

    Kuriakose S L, Devkota S, Rossiter D G, et al. Prediction of soil depth using environmental variables in an anthropogenic landscape, a case study in the Western Ghats of Kerala, India[J]. Catena, 2009, 79(1): 27-38.

    [11]

    李岩, 尚士友, 阿拉塔其其格, 等. 典型草原栗钙土层厚度空间插值方法研究[J]. 中国农机化学报, 2015, 36(1): 344~348. https://www.cnki.com.cn/Article/CJFDTOTAL-GLJH201501090.htm

    [12]

    杨阳, 李飒, 何福耀, 等. 半变异函数及取样间距对克里金法在海洋地层分析中的影响研究[J]. 工程地质学报, 2019, 27(4): 794-802. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201904012.htm

    [13]

    安永龙, 万利勤, 李霞, 等. 承德市土壤重金属空间结构与分布特征[J]. 水文地质工程地质, 2020, 47(6): 119-131. https://www.cnki.com.cn/Article/CJFDTOTAL-SWDG202006015.htm

    [14]

    乔冈, 徐友宁, 陈华清, 等. 宁东煤矿区地裂缝对植被生态环境的影响[J]. 地质通报, 2018, 37(12): 2176-2183. http://dzhtb.cgs.cn/gbc/ch/reader/view_abstract.aspx?file_no=20181207&flag=1

    [15]

    孟晖, 李春燕, 张若琳, 等. 全国地质环境承载能力评价[J]. 地质通报, 2021, 40(4): 451-459. http://dzhtb.cgs.cn/gbc/ch/reader/view_abstract.aspx?file_no=20210401&flag=1

    [16]

    史帅航, 白甲林, 余洋. 西南地区某矿产集采区土壤重金属迁移规律及生态风险评价[J]. 金属矿山, 2022, (2): 194-200. https://www.cnki.com.cn/Article/CJFDTOTAL-JSKS202202026.htm

    [17]

    陈飞香, 程家昌, 胡月明, 等. 基于RBF神经网络的土壤铬含量空间预测[J]. 地理科学, 2013, 33(1): 69-74. https://www.cnki.com.cn/Article/CJFDTOTAL-DLKX201301009.htm

    [18]

    谢梦姣, 王洋, 康营, 等. 人工神经网络与普通克里金插值法对土壤属性空间预测精度影响研究[J]. 生态与农村环境学报, 2021, 37(7): 934-942. https://www.cnki.com.cn/Article/CJFDTOTAL-NCST202107017.htm

    [19]

    Chen X Y, Liu D H, Yin P, et al. Temporal and spatial evolution of surface sediments characteristics in the Dagu River estuary and their dynamic response mechanism[J]. China Geology, 2019, (3): 325-332.

    [20]

    Ji Y K, Liu C L, Zhang Z, et al. Experimental study on characteristics of pore water conversion during methane hydrates formation in unsaturated sand[J]. China Geology, 2022, (5): 276-284.

    [21]

    邵海, 王英男, 殷志强, 等. 承德坝上高原如意河流域地表基质层调查与编图探索[J/OL]. 水文地质工程地质. 2022, 10.25. https://kns.cnki.net/kcms/detail/11.2202.p.20221025.1148.002.html.

    [22]

    王铭鑫, 范超, 高秉博, 等. 融合半变异函数的空间随机森林插值方法[J]. 中国生态农业学报, 2022, 30(3): 451-457. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTN202203010.htm

    ①

    殷志强, 邵海, 庞菊梅, 等. 承德资源环境承载能力综合地质调查与评价2021年延续报告. 中国地质环境监测院, 2020: 1-104.

    ②

    殷志强, 邢博, 邵海, 等. 支撑塞罕坝生态屏障建设水平衡和科学绿化研究取得新认识. 中国地质调查局《地质调查专报》, 2021.

    • 相关文章
  • 施引文献
  • 资源附件(0)
  • 加载中

图(3)

表(6)

计量
  • 文章访问数:  1003
  • PDF下载数:  64
  • 施引文献:  0
出版历程
收稿日期:  2022-05-29
修回日期:  2022-10-26
刊出日期:  2022-12-15

目录

    版权所有：中国地质调查局发展研究中心 copyright @2020
    返回