Numerical Simulation of Titanium Slag Flow Fluid-bed Chlorination in Spout Fluidized Bed
-
摘要:
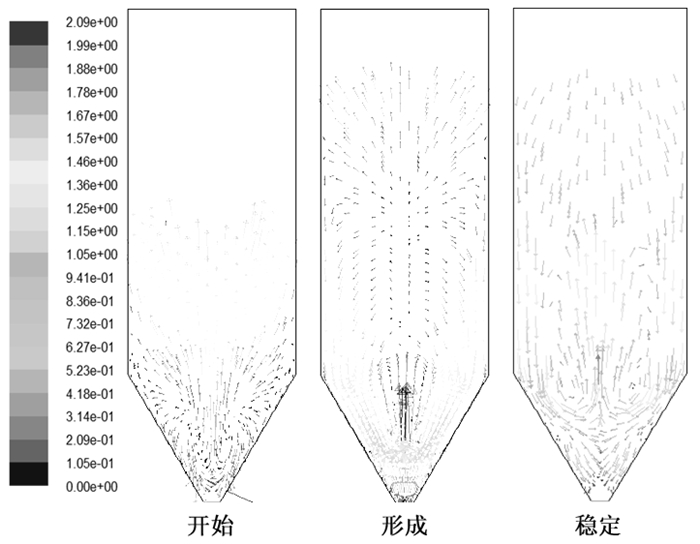
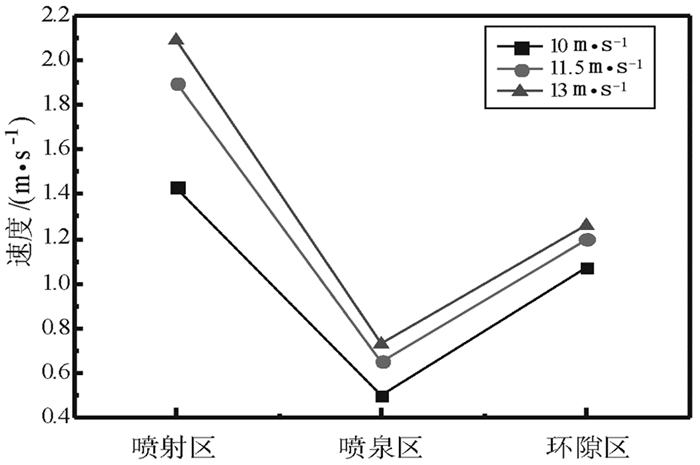
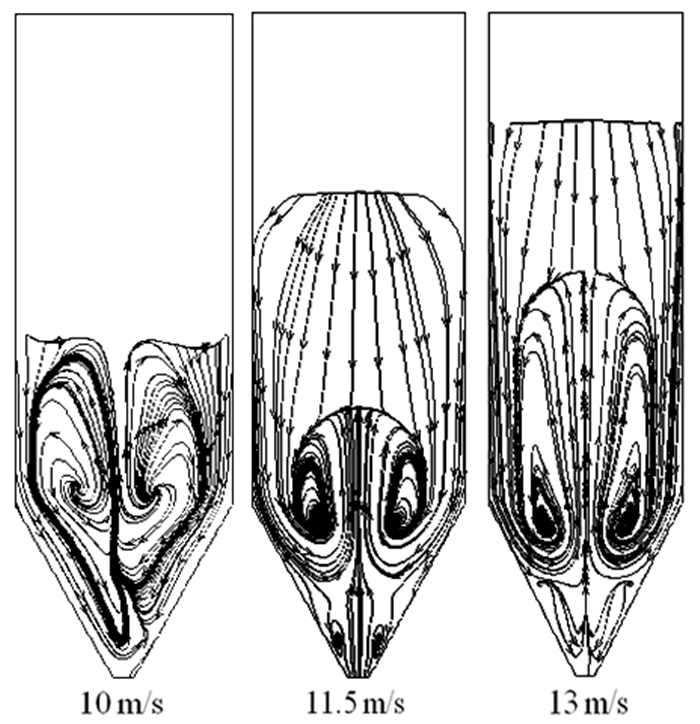
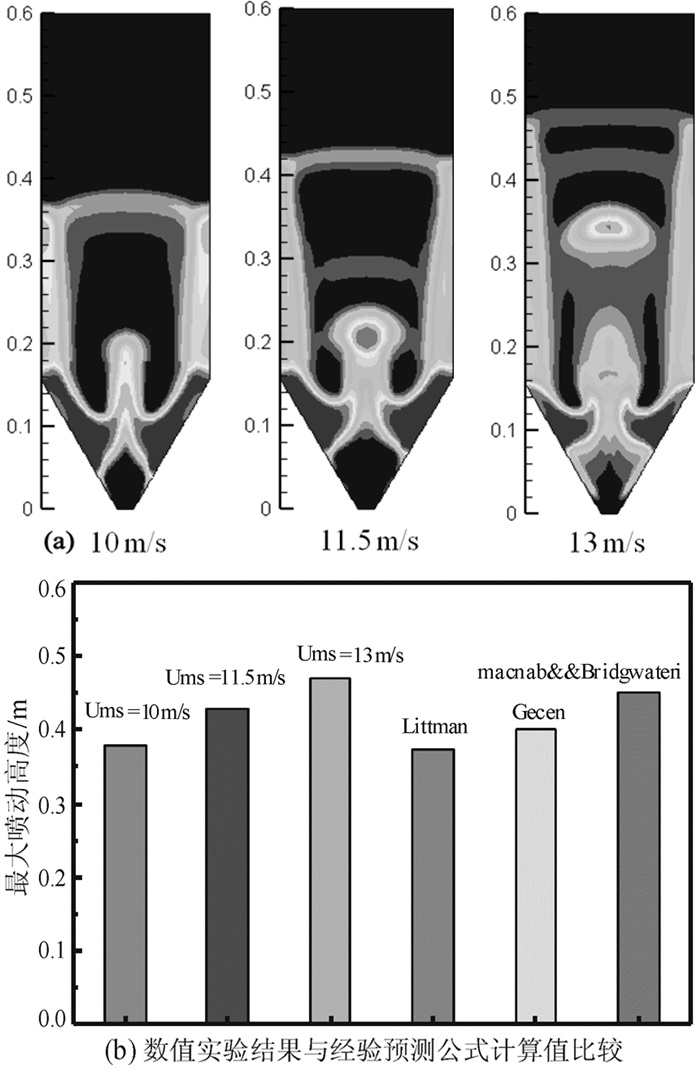
基于双流体模型和Gidaspow方程建立了预测钛渣喷动床沸腾氯化的数学模型。首先,采用经验计算公式得到了钛渣最小喷吹速度和最大喷吹高度,并对最小吹动速度进行了修正;其次,最小喷吹速度和相关边界条件为基础,运用Fluent软件模拟了钛渣喷动床沸腾氯化床内气固两相流的流体动力学特征;最后,分析了不同喷吹速度下气固两相流的流动特征和分区特征。结果表明:Gisher && Mathur公式更适合于钛渣喷动床沸腾氯化的最小喷动速度的预测;修正后的最小喷吹速度能够准确的模拟出钛渣喷动床沸腾氯化气固两相流的流体动力学特征;数值模拟得到的床内流动特征、分区的云图和矢量图、固体颗粒轨迹图和最大喷吹高度与相关研究结果一致。
Abstract:Based on Eulerian two-fluid model and Gidaspow model, a mathematic model for predicting the fluidized chlorination of titanium slag spouting fluidized bed was established. The minimum spouting speed and maximum spouting height of titanium slag spouted bed were obtained by empirical formula, meanwhile the minimum spouting speed was corrected. Then, Based on the minimum spouting speed and the related boundary conditions, hydrodynamic characteristics of gas-solid two-phase flow in titanium slag spouting fluidized bed was simulated by fluent software. At last, the flow characteristics and zoning characteristics of titanium slag spouting fluidized bed at different injection rates were analyzed. The results show that the Gisher && Mathur formula is more suitable for the prediction of the minimum spouting speed in titanium slag spouting fluidized bed. The modified minimum spouting speed can accurately simulate the hydrodynamic characteristics of titanium slag spouted bed. The numerical simulation of the hydrodynamic characteristics, the partition cloud and vector, the solid particle trajectory and the maximum spouting height were consistent with the relevant research results.
-
Key words:
- titanium slag /
- spouted bed /
- fluid-bed chlorination /
- numerical simulation
-

-
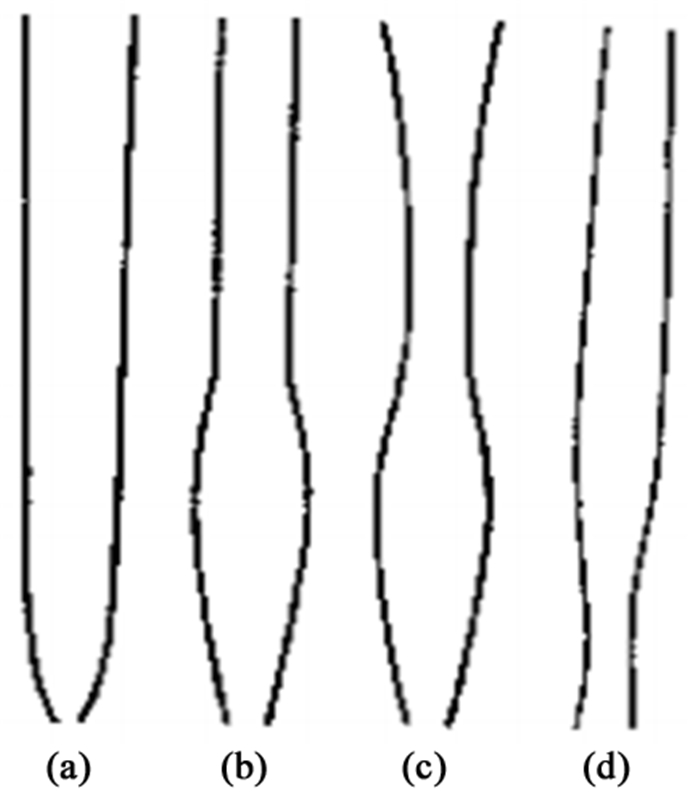
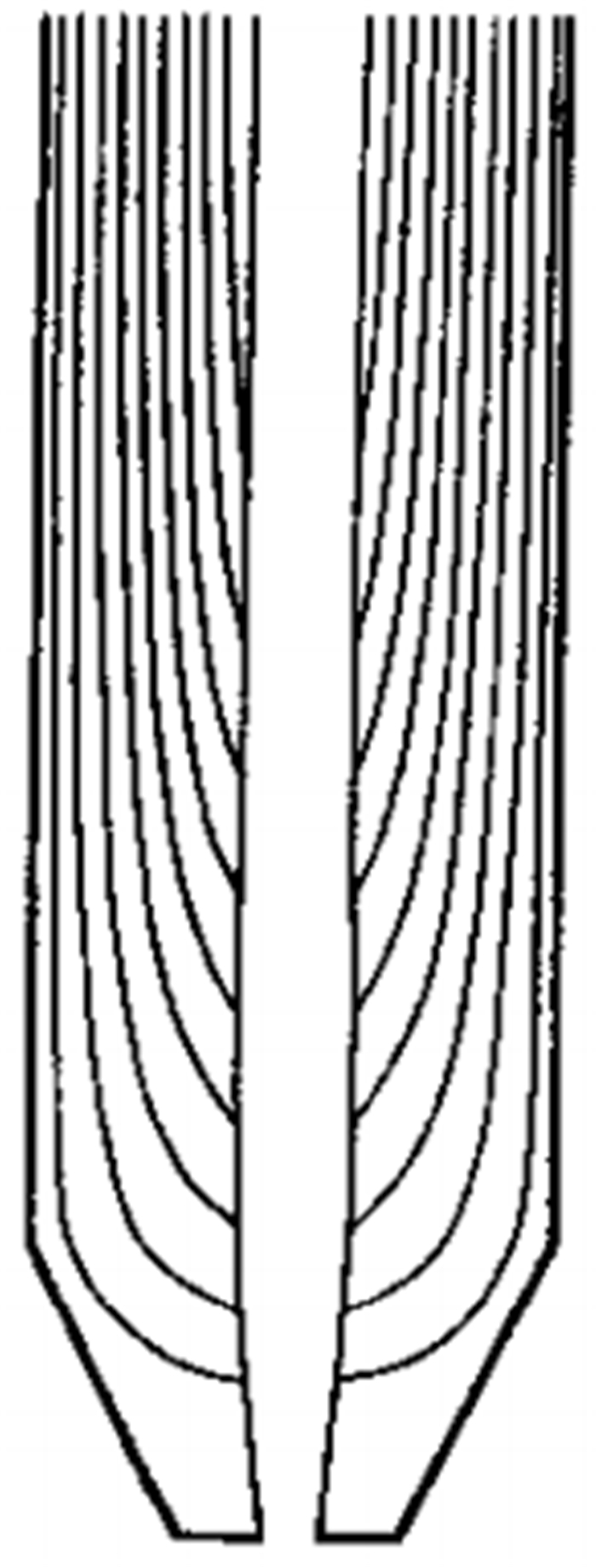
图 9 喷射区直径沿床层高度变化的4种形式[21]
Figure 9.
图 10 环隙区流线图[20]
Figure 10.
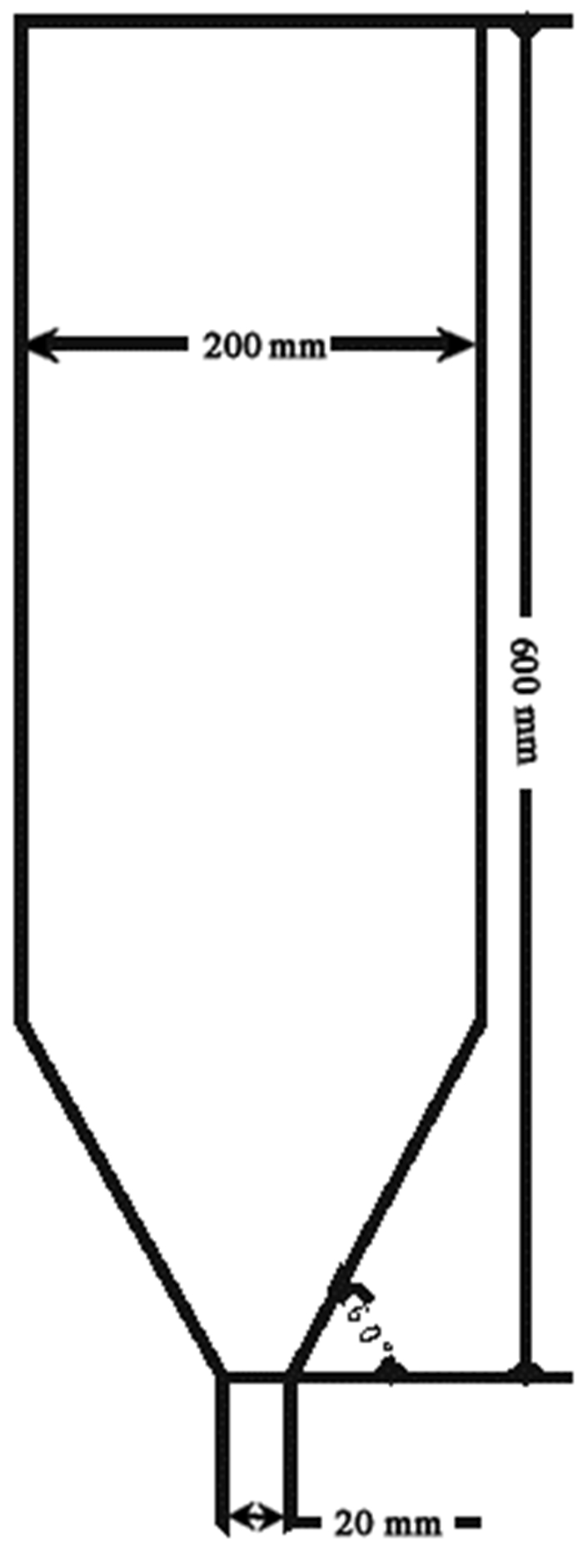
表 1 模拟计算的边界条件
Table 1. Boundary conditions for simulation calculation
边界条件 值 钛渣密度/(kg·m-3) 4 800 钛渣直径/m 1×10-3 钛渣初始体积分数 0.32 氯气的密度/(g·L-1) 3.17 初始静床高/m 0.24 网格数 19 200 曳力模型 Gidaspow 湍流模型 RNGk-ε 求解算法 Simple 内摩擦角 30° 恢复系数 0.95 时间步长 10-5 表 2 最小喷吹速度
Table 2. Minimum spouting velocity
研究者 经验计算公式 计算结果/(m·s-1) Gisher && Mathur[16] ${\frac{{{U_{ms}}}}{{\sqrt {2gH} }} = \left( {\frac{{{d_p}}}{{{D_c}}}} \right){{\left( {\frac{{{D_i}}}{{{D_c}}}} \right)}^{1/3}}{{\left( {\frac{{{\rho _p} - {\rho _f}}}{{{\rho _f}}}} \right)}^{1/2}}} $ 8.89 King && Harrison[17] $ {\frac{{{U_{ms}}}}{{\sqrt {2gH} }} = \left( {\frac{{{\rho _p}}}{{{\rho _p}}}} \right)\frac{{{d_p}}}{{{D_c}}}{{\left( {\frac{{{D_i}}}{{{D_c}}}} \right)}^{1/3}}{{\left( {\frac{{{\rho _p} - {\rho _f}}}{{{\rho _f}}}} \right)}^{1/2}}}$ 2.14 Fane && Mitchell[18] $ {\frac{{{U_{ms}}}}{{\sqrt {2gH} }} = \left( {0.2D_c^*} \right)\frac{{{d_p}}}{{{D_c}}}{{\left( {\frac{{{D_i}}}{{{D_c}}}} \right)}^{1/3}}{{\left( {\frac{{{\rho _p} - {\rho _f}}}{{{\rho _f}}}} \right)}^{1/2}}}$ 0.42 Wen-Yu[10] ${\frac{{{d_p}{u_{mf}}{\rho _g}}}{{{\mu _g}}} = {\rm{ }}{{\left[ {C^2_1 + {C_2}\frac{{d^3_p{\rho _g}\left( {{\rho _p} - {\rho _g}} \right)g}}{{{\mu ^2}}}} \right]}^{1/2}}} $ 7.86 表 3 最大喷动高度
Table 3. Maximum spoutable bed height
研究者 经验计算公式 计算结果/m Mcnab&&Bridgwaterti[19] ${{H_m} = \frac{{D^2_c}}{{{d_P}}}{{\left( {\frac{{{D_c}}}{{{D_i}}}} \right)}^{2/3}}\frac{{568{b^2}}}{{Ar}}{{\left( {\sqrt {1 + 35.9 \times {{10}^{ - 6}}Ar} - 1} \right)}^2}} $ 0.45 Littman[20] $ {\frac{{{H_m}{d_p}}}{{{D^2} - d^2_p}} = 0.345{{\left( {\frac{{{d_p}}}{D}} \right)}^{ - 0.384}}}$ 0.373 Cecen[21] ${\frac{{{H_m}{d_p}}}{{{D^2}}} = 0.99{{\left( {\frac{{{D_i}}}{D}} \right)}^{0.856}}{{\left( {\frac{{{\rho _p} - \rho }}{\rho }\frac{{g{D_i}}}{{{u_{mf}}{u_t}}}} \right)}^{0.144}}} $ 0.4 -
[1] 刘禹明, 王伟, 钱鑫.大型无筛板沸腾氯化技术及装备的研发与应用[J].钛工业进展, 2014(1):35-37. http://www.wenkuxiazai.com/doc/9cacbc71cfc789eb162dc802.html
[2] 杨平, 陈德明.攀枝花钛渣组合式流化床氯化制备TiCl4的研究[J].钢铁钒钛, 2007, 28(2):48-52. doi: 10.7513/j.issn.1004-7638.2007.02.010
[3] 马崇振.攀枝花某铁尾矿提钛降杂试验研究[J].矿产保护与利用, 2016(5):74-78. http://kcbh.cbpt.cnki.net/WKD/WebPublication/paperDigest.aspx?paperID=d57e88f3-f8a2-4bf3-947b-ec8e3842f091
[4] 成文江.人造金红石加入量对沸腾氯化工艺的影响[J].中国有色金属, 2006(12):68-69. http://www.wenkuxiazai.com/doc/fc059225a5e9856a56126038-2.html
[5] 牛丽萍, 张延安, 吕国志, 等.天然金红石粉体沸腾氯化工艺条件优化研究[J].过程工程学报, 2011, 11(6):1002-1009. http://www.oalib.com/paper/4753855
[6] 金涌.流态化工程原理[M].北京:清华大学出版社, 2002.
[7] Rüdisüli M, Schildhauer T J, Biollaz S M A, et al. Bubble characterization in a fluidized bed by means of optical probes[J]. International Journal of Multiphase Flow, 2012, 41(2):56-67. https://www.sciencedirect.com/science/article/pii/S0301932212000031
[8] Yuan P T, Gidaspow D. Computation of flow patterns in circulating fluidized beds[J]. Aiche Journal, 1990, 36(6):885-896. doi: 10.1002/(ISSN)1547-5905
[9] Felice R D. The voidage function for fluid-particle interaction systems[J]. International Journal of Multiphase Flow, 1994, 20(1):153-159. doi: 10.1016/0301-9322(94)90011-6
[10] Wen C Y, Yu Y H. Mechanics of fluidization[J]. Chem. Engng Prog. Symp. Ser, 1966, 62:100-111. http://www.oalib.com/references/15294141
[11] Ergun S. Fluid flow through packed columns[J]. Chem. Eng. Prog, 1952, 48(2):89-94. https://www.researchgate.net/publication/273128396_Fluid_Flow_Through_Packed_Column
[12] And D L K, Hill R J. Inertial effects in suspension and porous-media flows [J]. Annual Review of Fluid Mechanics, 2003, 33(1):619-647. http://www.annualreviews.org/doi/abs/10.1146/annurev.fluid.33.1.619
[13] Beetstra R, Vander Hoef M, Kuipers J. Numerical study of segregation using a new drag force correlation for polydisperse systems derived from lattice-Boltzmann simulations[J]. Chemical Engineering Science, 2007, 62 (1):246-255. https://www.sciencedirect.com/science/article/pii/S0009250906005008
[14] Gidaspow D. Multiphase Flow and Fluidization[J]. Multiphase Flow & Fluidization, 1994(95):1-29. https://www.elsevier.com/books/multiphase-flow-and-fluidization/gidaspow/978-0-08-051226-6
[15] Zheng Z, Lin L, Chen Z. A dual-scale lattice gas automata model for gas-solid two-phase flow in bubbling fluidized beds[J]. Computers & Mathematics with Applications, 2011, 61(12):3593-3605. https://www.sciencedirect.com/science/article/pii/S0898122111000472
[16] Li T, Gopalakrishnana P, Garg R, et al. CFD-DEM study of effect of bed thickness for bubbling fluidized beds[J]. Particuology, 2012, 10(5):532-541. doi: 10.1016/j.partic.2012.02.006
[17] Goldschmidt M J V, Kuipers J A M, Swaaij W P M V, Hydrodynamic modelling of dense gas-fluidised beds using the kinetic theory of granular flow: effect of coefficient of restitution on bed dynamics[J]. Chemical Engineering Science, 2001, 56(2):571-578. doi: 10.1016/S0009-2509(00)00262-1
[18] Fane A G, Mitchell R A. Minimum spouting velocity of scaled-up beds[J]. Canadian Journal of Chemical Engineering, 2010, 62(3):437-439. http://onlinelibrary.wiley.com/doi/10.1002/cjce.5450620325/pdf
[19] Mcnab G S, Bridgwater J. A theory for effective solid stresses in the annulus of a spouted bed[J]. Canadian Journal of Chemical Engineering, 1979, 57(3):274-279. https://www.researchgate.net/publication/230360881_A_Theory_for_Effective_Solid_Stresses_in_the_Annulus_of_Spouted_Beds
[20] Iii M H M, Littman H. Predicting the maximum spoutable height in spouted beds of irregularly shaped particles[J]. Industrial & Engineering Chemistry Fundamentals, 1982, 21(1):23-26. http://eng.rpi.edu/faculty/howard-littman
[21] Çeçen A. The maximum spoutable bed heights of fine particles spouted with air[J]. Canadian Journal of Chemical Engineering, 2010, 72(5):792-797. http://onlinelibrary.wiley.com/doi/10.1002/cjce.5450720504/full
[22] B Ye, C J Lim, J R Grace. Hydrodynamics of spouted and spout-fluidized beds at high temperature[J]. Canadian Journal of Chemical Engineering, 1992, 70(5):840-847. doi: 10.1002/cjce.v70:5
[23] Hosseini S H, Fattahi M, Ahmadi G. Hydrodynamics studies of a pseudo 2D rectangular spouted bed by CFD[J]. Powder Technology, 2015, 27(9):301-309. https://www.sciencedirect.com/science/article/pii/S0032591015002879
[24] S H Hosseini, G Ahmadi, M Olazar. CFD study of particle velocity profiles inside a draft tube in a cylindrical spouted bed with conical base[J]. Taiwan Inst. Chem.Eng. 2014, 45:2140-2149. doi: 10.1016/j.jtice.2014.05.027
[25] Mathur K B, Epstein N. Developments in spouted bed technology[J]. Canadian Journal of Chemical Engineering, 1974, 52(2):129-144. doi: 10.1002/cjce.v52:2
[26] Shuyan Wang, Baoli Shao, Rui Liu, et al. Comparison of numerical simulations and experiments in conical gas-solid spouted bed[J]. Chinese Journal of Chemical Engineering, 2015, 23(10):1579-1586. doi: 10.1016/j.cjche.2015.07.006
-



 下载:
下载: