Flow pattern analysis around a solid cylinder with both porous and water rings in porous media
-
摘要:
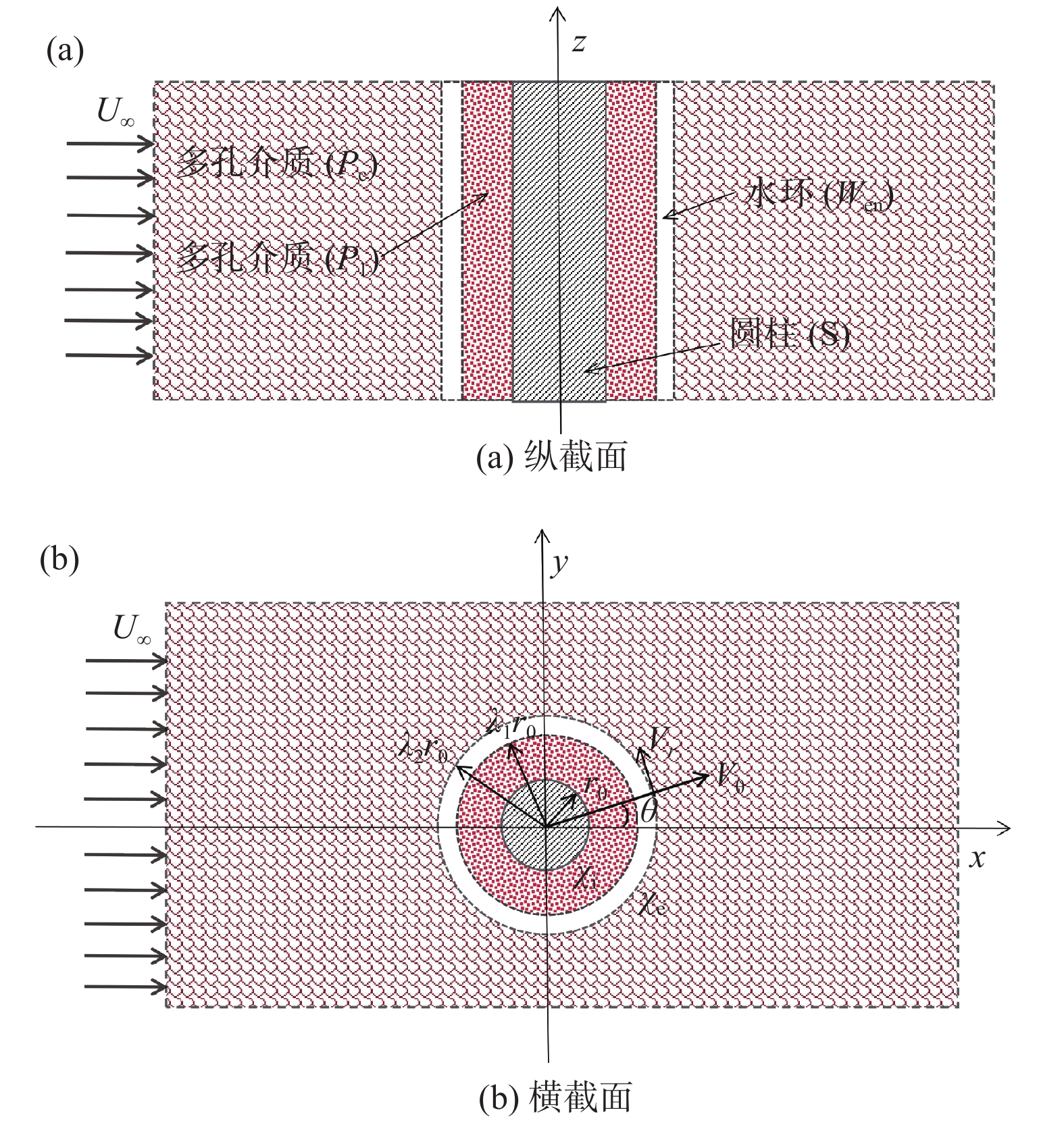
对二维无限大多孔介质内单向均匀水平流垂直绕过“固体小圆柱-多孔介质环-水环-多孔介质”复杂四层结构下的流场进行了解析求解。内、外多孔介质区域均采用Brinkman模型,纯流体水环采用Stokes模型,通过耦合界面间的质量、动量守恒关系得到了各区域流函数的通用表达式。在此基础上分析了不同几何参数,不同内、外多孔介质渗透系数情况下,圆柱外绕流的流型变化;着重研究了水环间隙以及内、外多孔介质渗透系数的变化对流型及横向、纵向速度分布的影响。结果表明:外部多孔区流型主要受控于外部渗透系数;水环间隙宽度对水环内速度峰值影响较大;内部渗透系数增加到某一临界值情况下,横截面速度分布从阶梯形变为抛物形,即“穿透”现象。研究结果对有类似结构的地埋管换热器、地下水污染物吸收装置、地下水测速装置等的设计研发有理论指导意义。
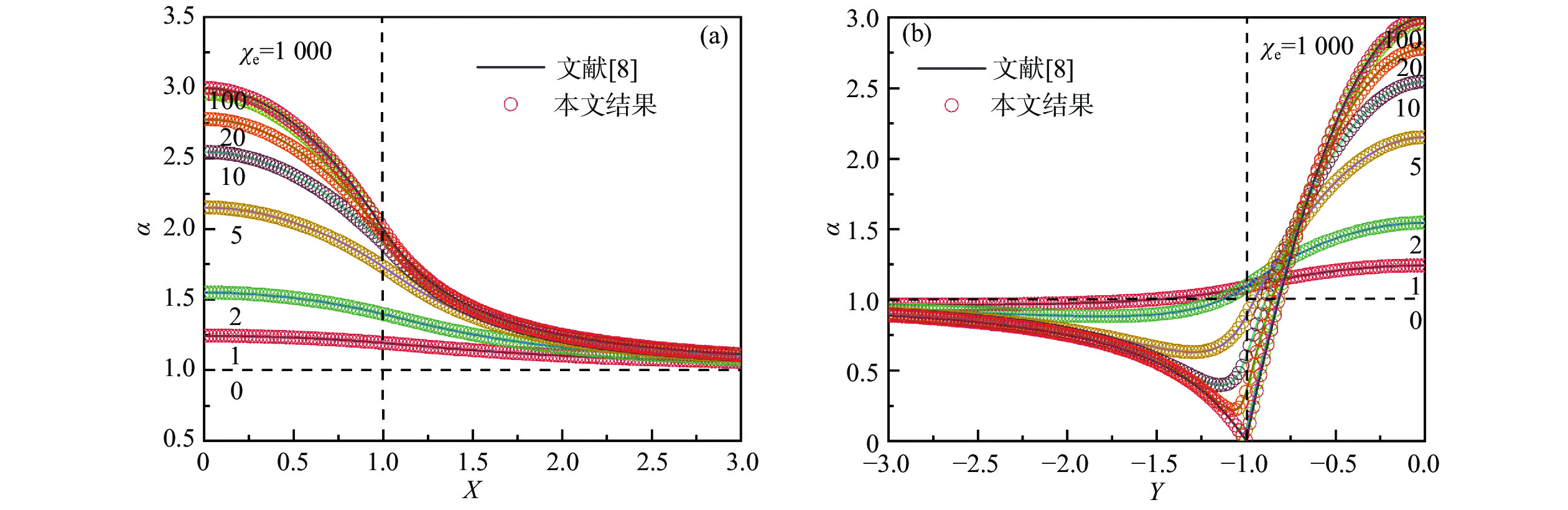
Abstract:The flow field around a solid cylinder with both porous and water rings embedded vertically in an infinite large porous media is analytically simulated. The Brinkman model are applied for both the internal porous ring and external infinite large porous media. The Stokes model is used for the open water ring. By coupling the mass and momentum conservations at the interfaces between different regions, a general set of stream function equations can be derived. The program code is firstly validated by comparing the results of a typical two layer case with those of the previous literature. Then, the flow patterns for this complicated multilayer coaxial structure is analytically simulated by giving different geometric parameters and different coefficients of permeability of the inner and outer porous media. The influences of the width of the water ring gap and the coefficients of permeability of the internal and external porous media on the flow patterns and the velocity distribution of vertical and horizontal profiles are also emphatically studied. The results show that the flow pattern in the external porous zone is mainly controlled by its permeability. The width of the water ring has a great influence on the peak value of the velocity profile in the vertical cross section. With the increasing coefficient of permeability of the internal porous zone to a critical value, the velocity profile in the cross section will change from a step-shaped pattern to a parabolic one, which is viewed as a penetration phenomenon. It is believed that these obtained results are helpful in guiding a design such as borehole heat exchanger, groundwater pollutant absorption device, groundwater velocity measurement device, etc., with similar geometrical configuration.
-
Key words:
- porous media /
- water ring /
- flow around /
- analytical solution /
- flow pattern
-

-
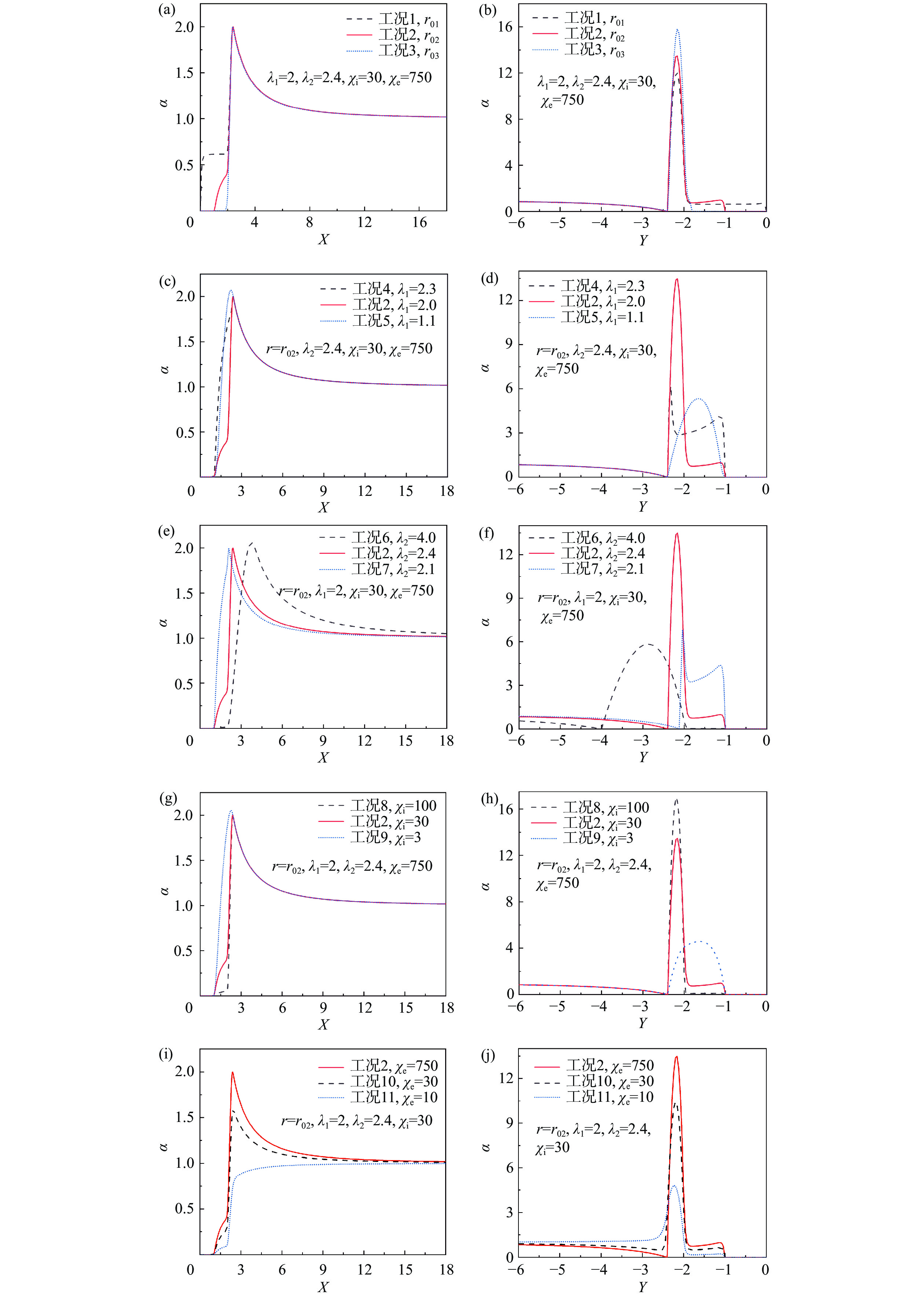
表 1 不同工况的计算参数
Table 1. Summary of calculation conditions under different parameters.
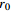
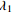
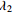
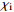
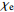
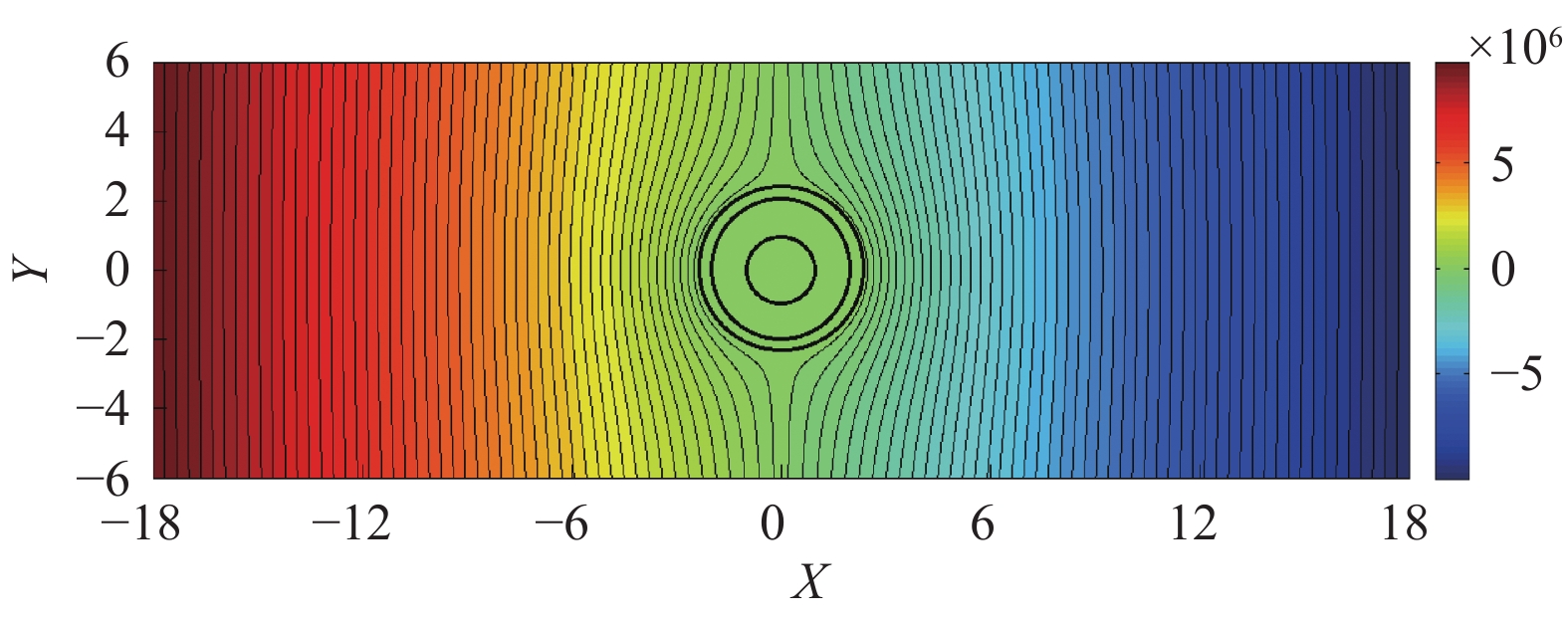
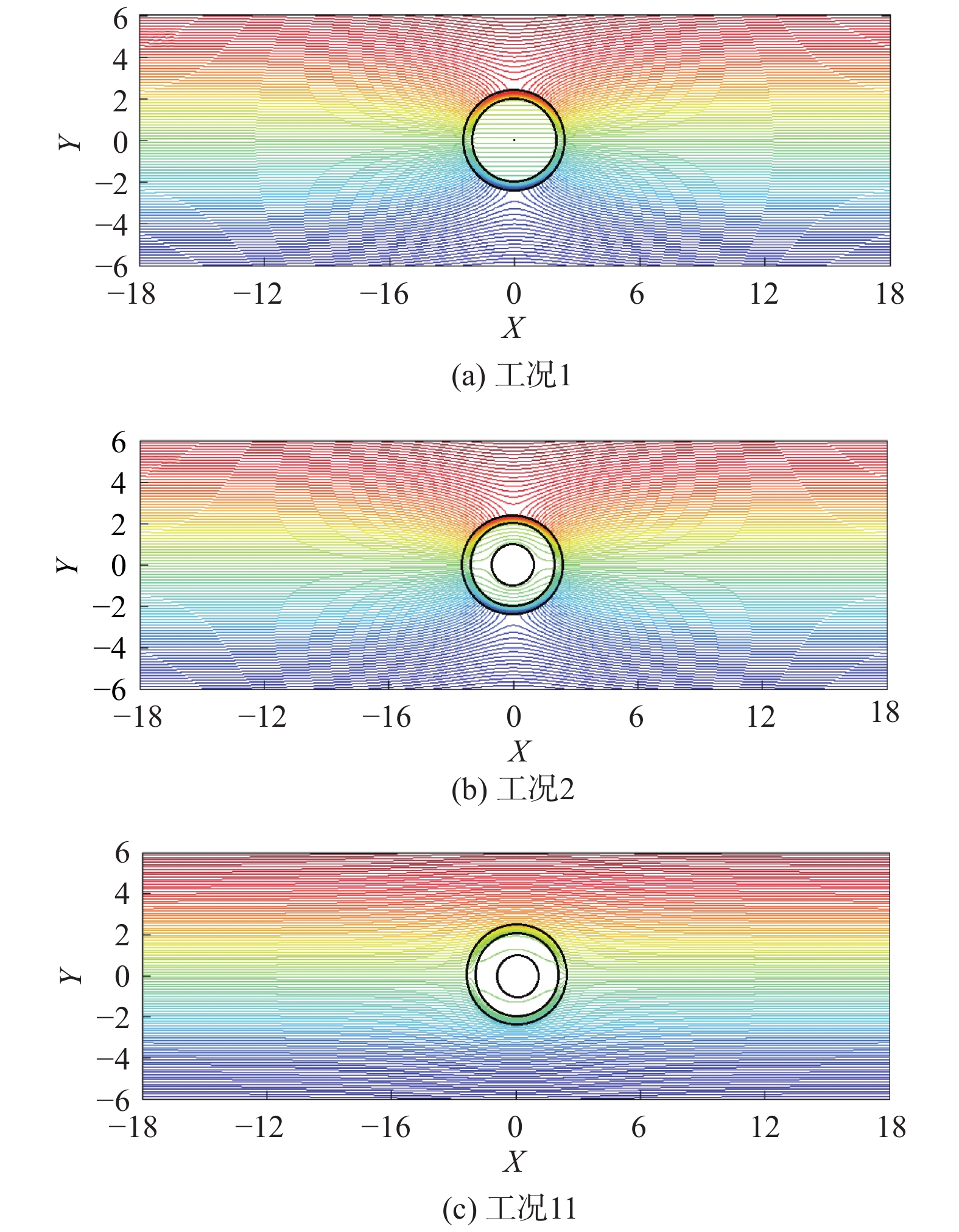
工况1 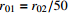
100 120 0.6 15 工况2 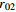
2 2.4 30 750 工况3 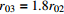
1.1 1.32 54 1350 工况4 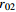
2.3 2.4 30 750 工况5 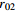
1.1 2.4 30 750 工况6 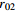
2 4.0 30 750 工况7 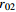
2 2.1 30 750 工况8 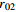
2 2.4 100 750 工况9 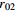
2 2.4 3 750 工况10 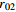
2 2.4 30 30 工况11 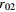
2 2.4 30 10 -
[1] 陈崇希, 胡立堂. 渗流-管流耦合模型及其应用综述[J]. 水文地质工程地质,2008,35(3):70 − 75. [CHEN Chongxi, HU Litang. A review of the page pipe coupling model and its application[J]. Hydrogeology & Engineering Geology,2008,35(3):70 − 75. (in Chinese with English abstract) doi: 10.3969/j.issn.1000-3665.2008.03.018
[2] RASHIDI S, TAMAYOL A, VALIPOUR M S, et al. Fluid flow and forced convection heat transfer around a solid cylinder wrapped with a porous ring[J]. International Journal of Heat & Mass Transfer,2013,63:91 − 100.
[3] SWARTZ M A, FLEURY M E. Interstitial flow and its effects in soft tissues[J]. Annual Review of Biomedical Engineering,2007,9(1):229 − 256. doi: 10.1146/annurev.bioeng.9.060906.151850
[4] POP I, INGHAM D B. Flow past a sphere embedded in a porous medium based on the Brinkman model[J]. International Journal of Engineering Science,1992,30(2):257 − 262. doi: 10.1016/0020-7225(92)90058-O
[5] DROST W, KLOTZ D, KOCH A, et al. Point dilution methods of investigating ground water flow by means of radioisotopes[J]. Water Resources Research,1968,4(1):125 − 146. doi: 10.1029/WR004i001p00125
[6] SANO O. Viscous flow past a cylindrical hole bored inside porous media-with application to measurement of the velocity of subterranean water by the single boring method[J]. Nagare,1983,2(3):252 − 259.
[7] MOMII K, JINNO K, HIRANO F. Laboratory studies on a new laser Doppler Velocimeter System for horizontal groundwater velocity measurements in a borehole[J]. Water Resources Research,1993,29(2):283 − 291. doi: 10.1029/92WR01958
[8] RAJA SEKHAR G P, SANO O. Viscous flow past a circular/spherical void in porous media-an application to measurement of the velocity of groundwater by the single boring method[J]. Journal of the Physical Society of Japan,2000,69(8):2479 − 2484. doi: 10.1143/JPSJ.69.2479
[9] RAJA SEKHAR G P, SANO O. Two-dimensional viscous flow past a slightly deformed circular cavity in a porous medium[J]. Fluid Dynamics Research,2001,28(4):281 − 293. doi: 10.1016/S0169-5983(00)00033-2
[10] RAJA SEKHAR G P, SANO O. Two-dimensional viscous flow in a granular material with a void of arbitrary shape[J]. Physics of Fluids,2003,15(2):554 − 567. doi: 10.1063/1.1536165
[11] LI Y C, PARK C W. A predictive model for the removal of colloidal particles in fibrous filter media[J]. Chemical Engineering Science,1999,54(5):633 − 644. doi: 10.1016/S0009-2509(98)00266-8
[12] SEKHAR G P R. Effective medium model for flow through beds of porous cylindrical fibres[J]. Applicable Analysis,2010,89(6):833 − 848. doi: 10.1080/00036811003649116
[13] BAYER-RAICH M, CREDOZ A, GUIMERÀ J, et al. Estimates of horizontal groundwater flow velocities in boreholes[J]. Groundwater,2019,57(4):525 − 533. doi: 10.1111/gwat.12820
[14] KLAMMLER H, HATFIELD K, ANNABLE M D, et al. General analytical treatment of the flow field relevant to the interpretation of passive fluxmeter measurements[J]. Water Resources Research,2007,43(4):264 − 272.
[15] BECKERMANN C, VISKANTA R, RAMADHYANI S. Natural convection in vertical enclosures containing simultaneously fluid and porous layers[J]. Journal of Fluid Mechanics,1988,186:257 − 284. doi: 10.1017/S0022112088000138
[16] 戴传山, 祁芸芝, 雷海燕, 等. 悬浮微小颗粒对多孔介质渗流特性影响的实验研究[J]. 水文地质工程地质,2016,43(6):1 − 6. [DAI Chuanshan, QI Yunzhi, LEI Haiyan, et al. Deposition effect of suspended microparticle on the local permeability in porous media[J]. Hydrogeology & Engineering Geology,2016,43(6):1 − 6. (in Chinese with English abstract)
[17] RAJA SEKHAR G P, AMARANATH T. Stokes flow inside a porous spherical shell[J]. Zeitschrift Fur Angewandte Mathematik Und Physik ZAMP,2000,51(3):481 − 490. doi: 10.1007/s000330050009
[18] BRINKMAN H C. A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles[J]. Flow, Turbulence & Combustion,1949,1(1):27 − 34.
[19] PADMAVATHI B S, AMARANATH T, NIGAM S D. Stokes flow past a porous sphere using Brinkman's model[J]. Zeitschrift Für Angewandte Mathematik Und Physik ZAMP,1993,44(5):929 − 939.
[20] QIN Y, KALONI P N. Creeping flow past a porous spherical shell[J]. ZAMM Journal of Applied Mathematics and Mechanics,1993,73(2):77 − 84. doi: 10.1002/zamm.19930730207
-



 下载:
下载: