Reliability analysis based on joint uncertainty: A case study of a rock slope in Tibet
-
摘要:
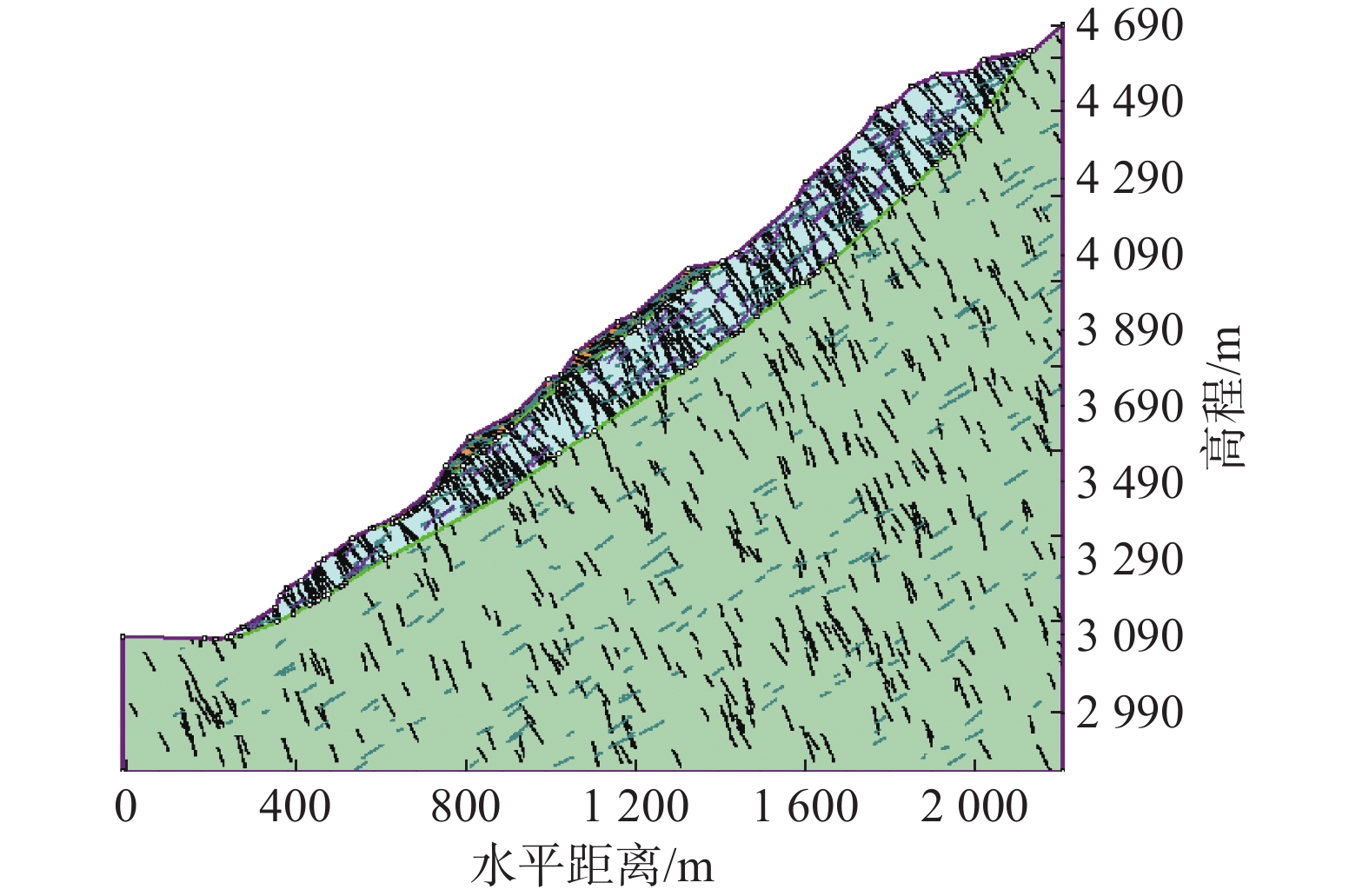
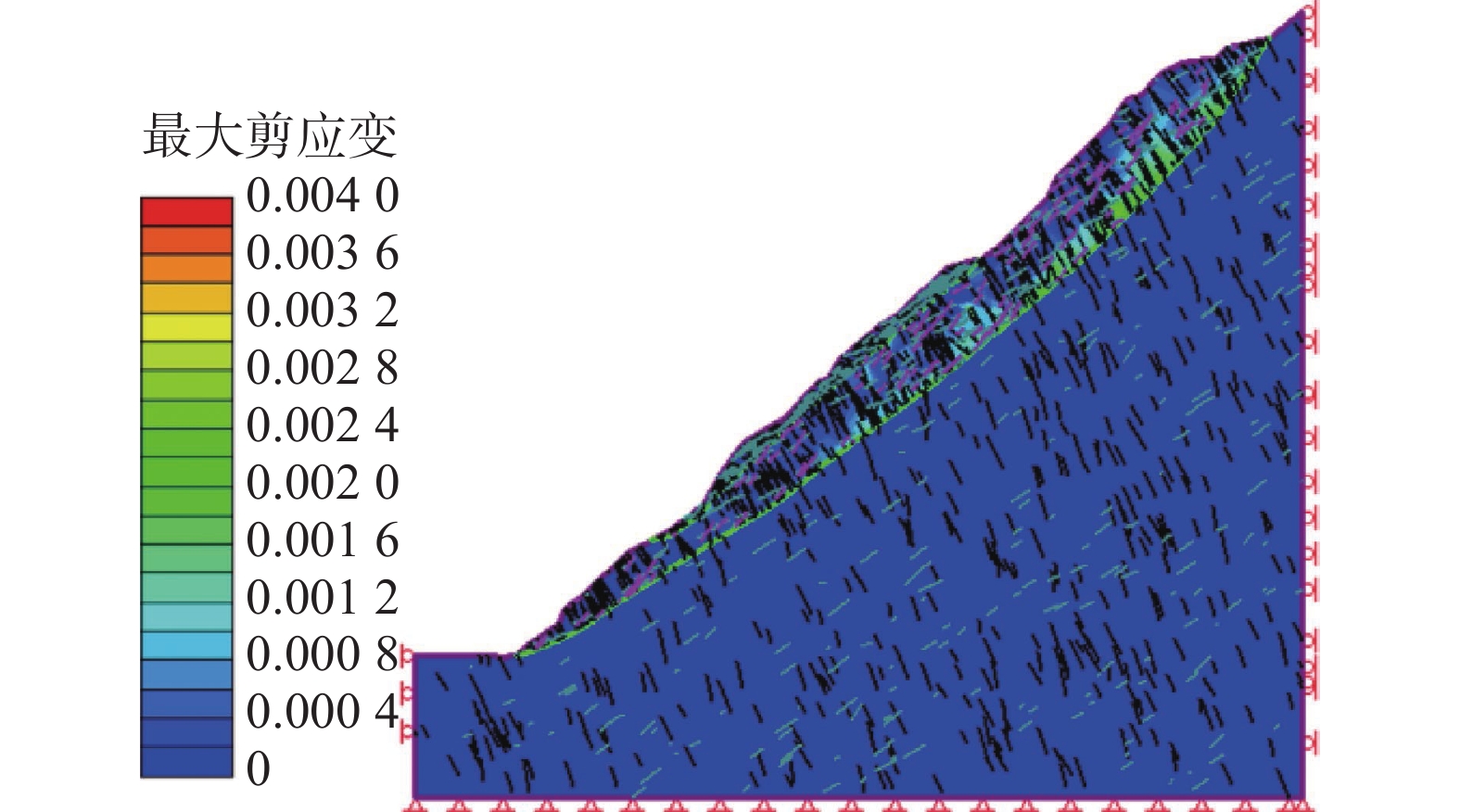
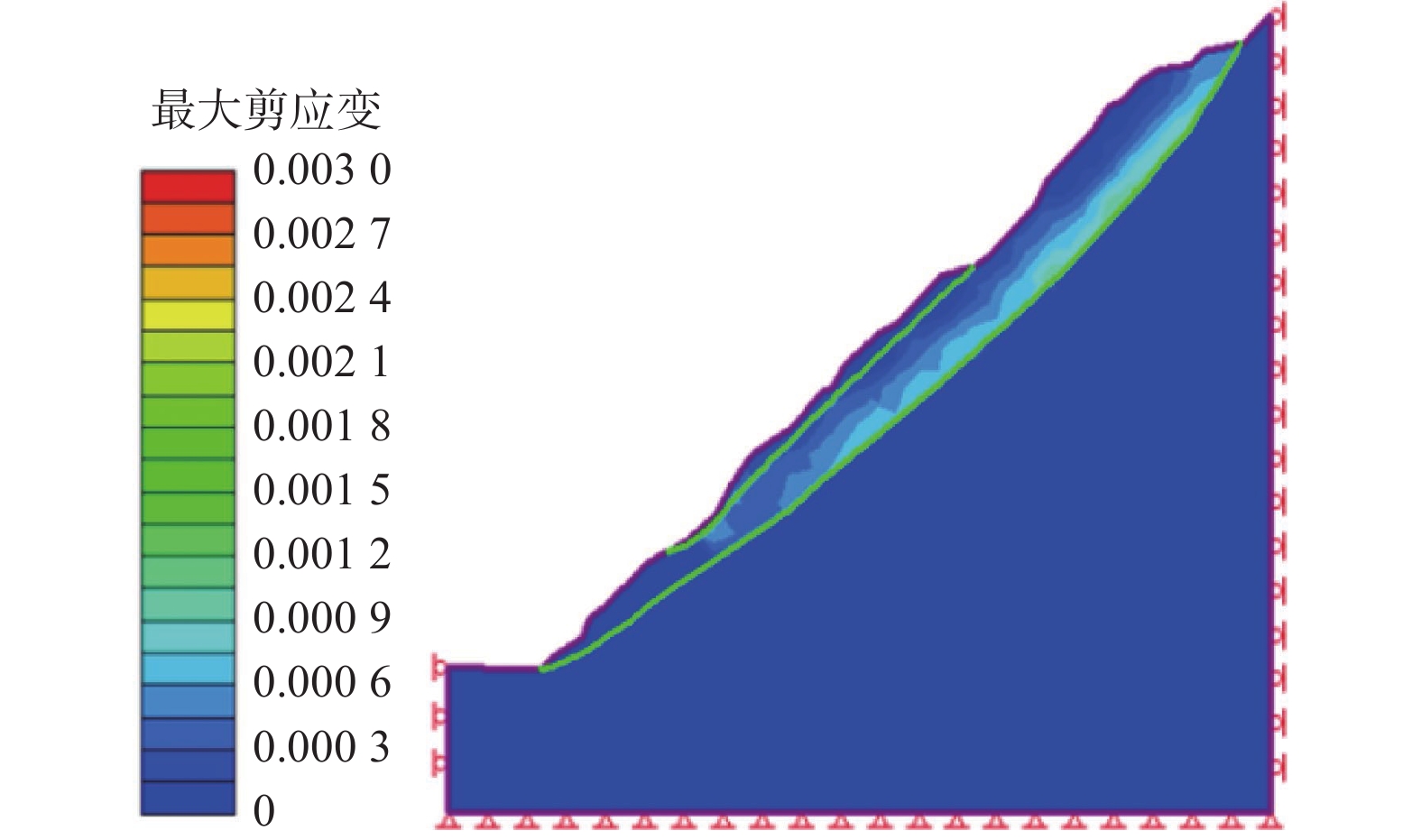
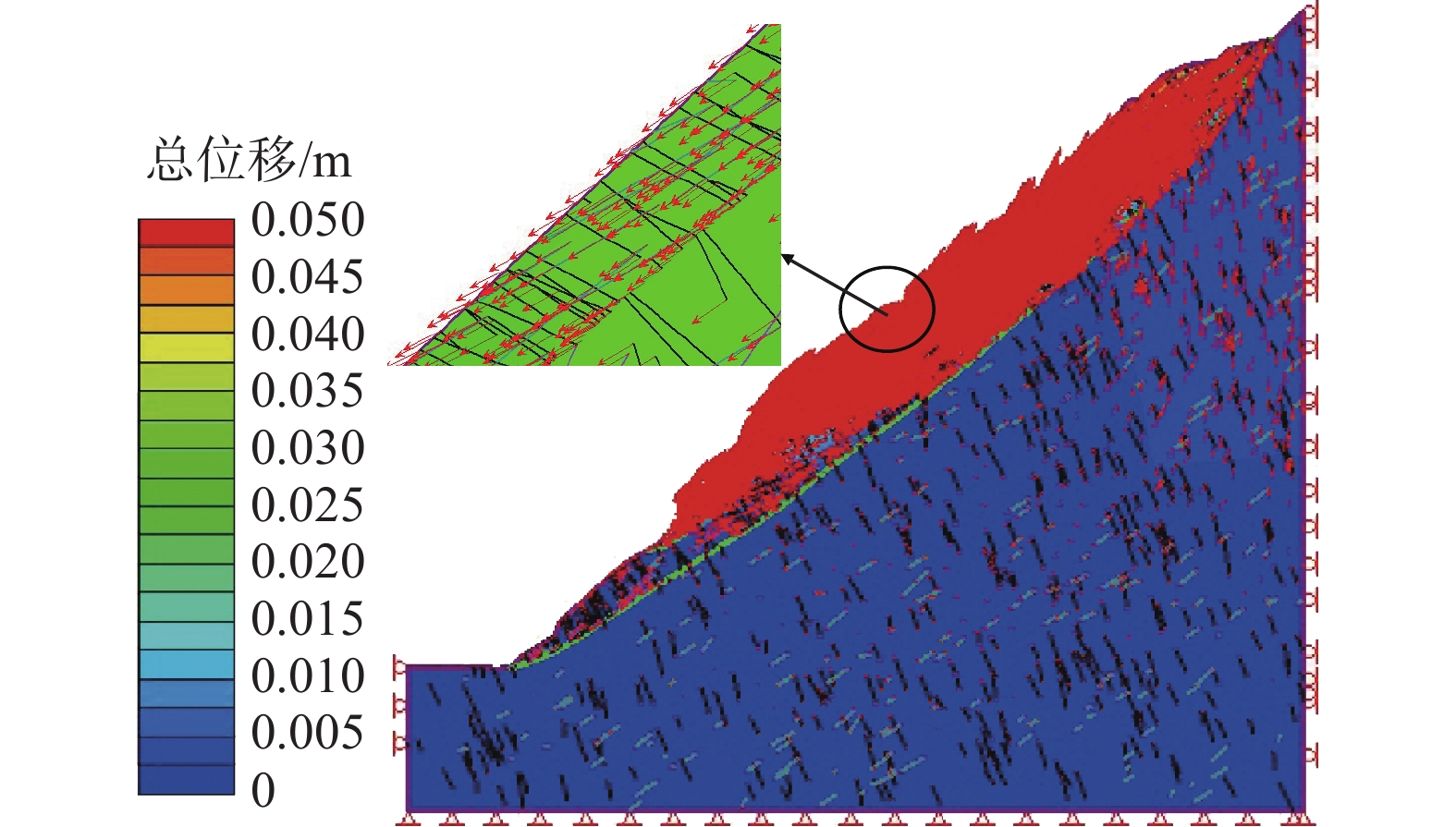
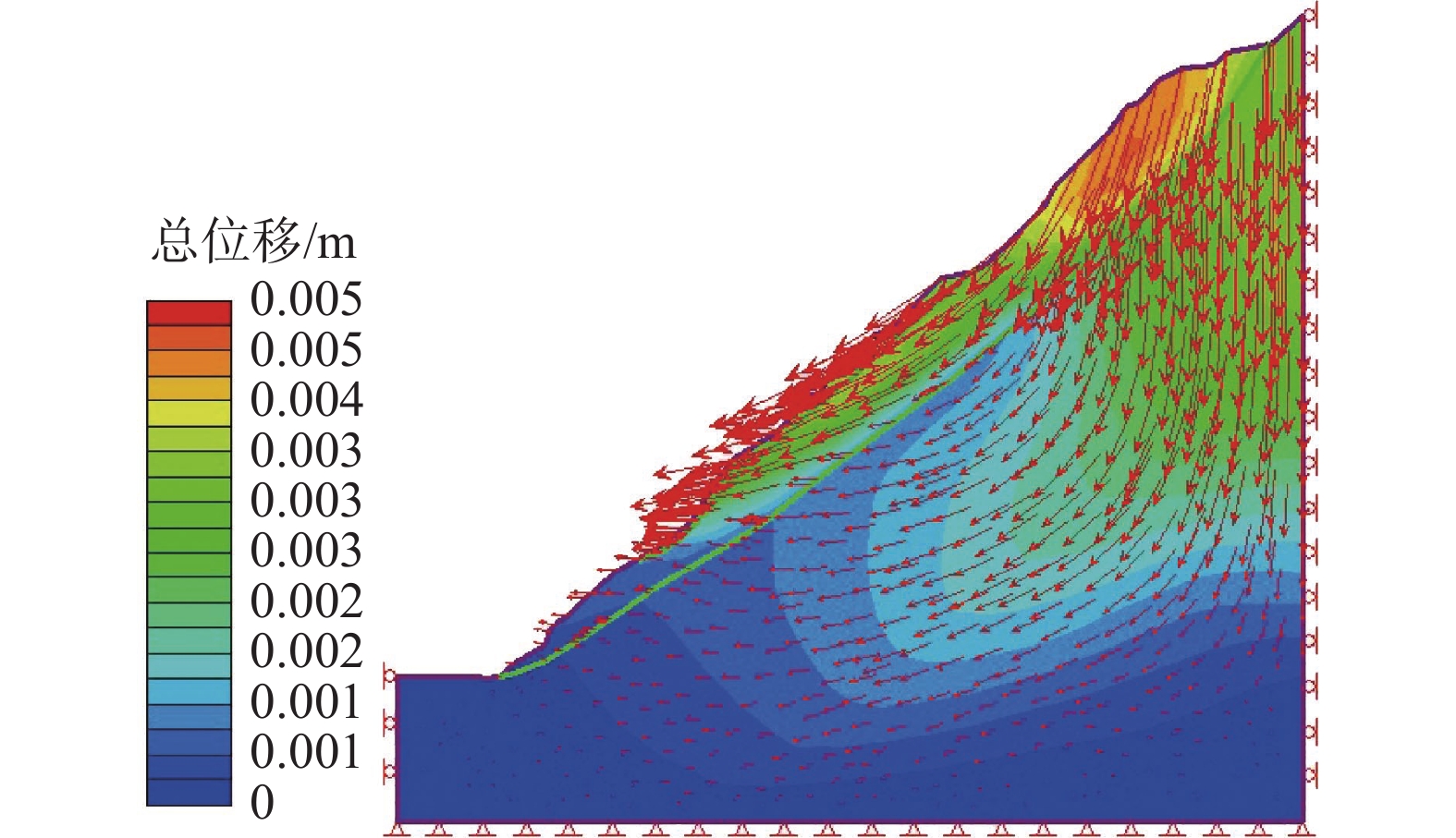
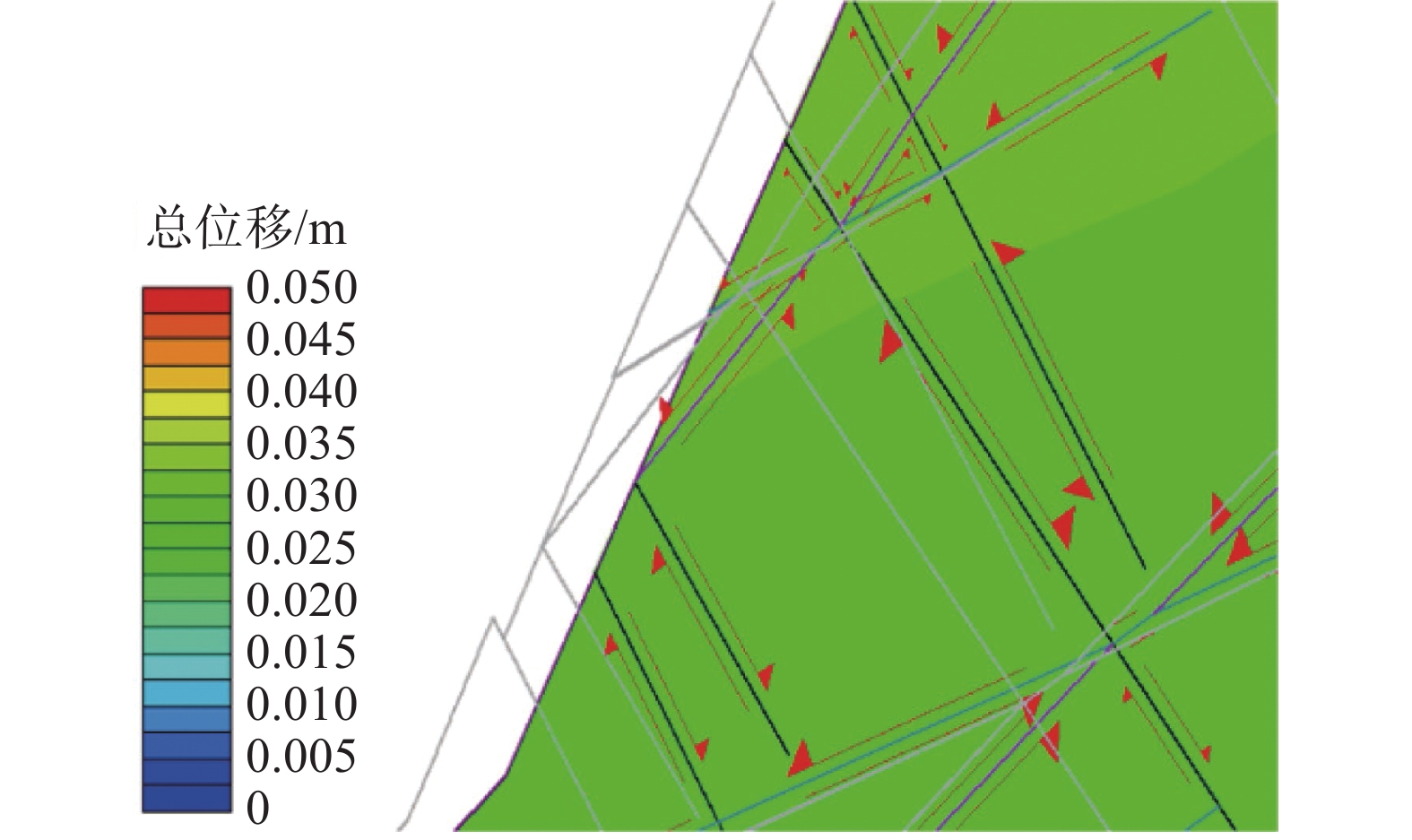
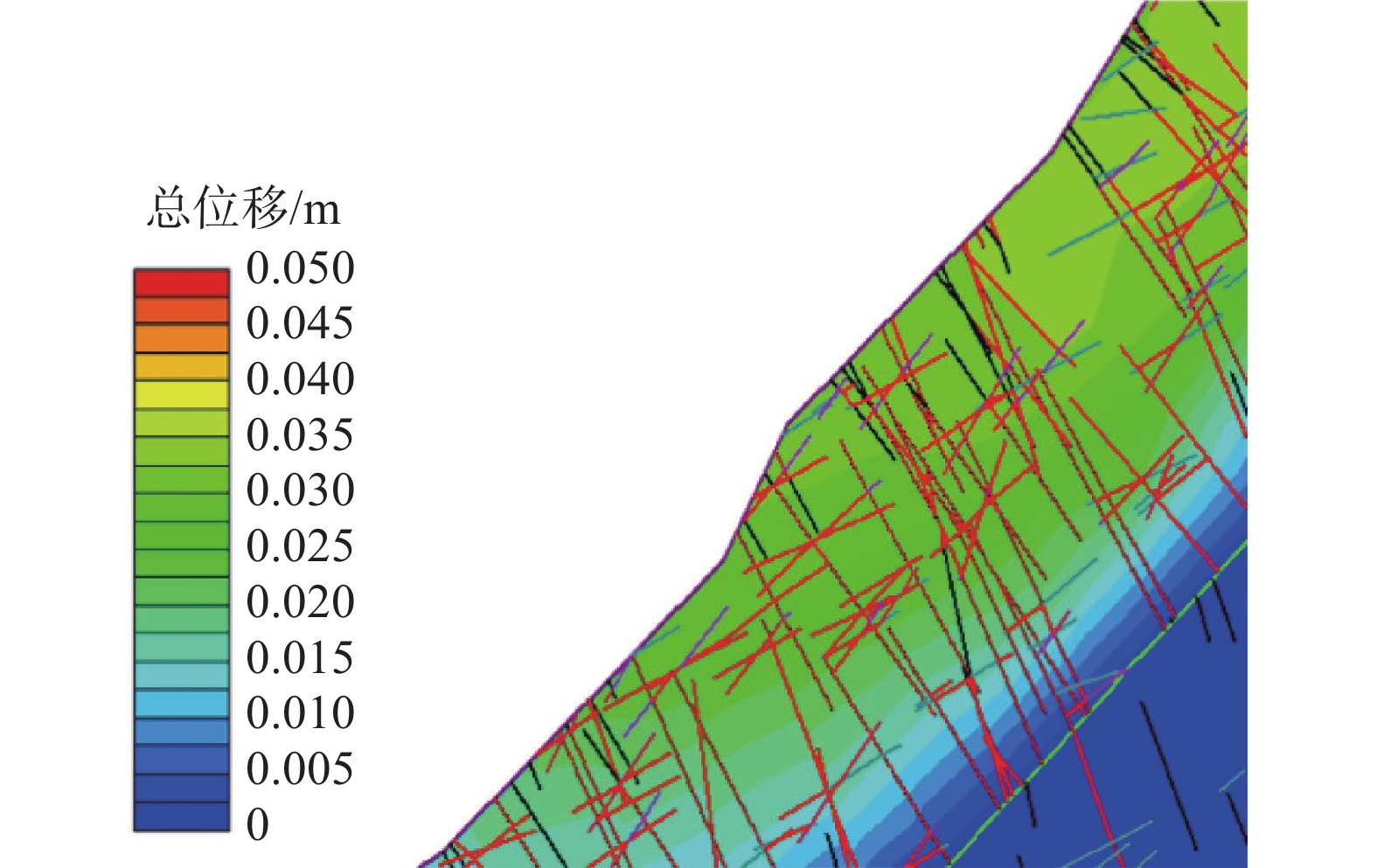
边坡稳定性一直是边坡安全的重点研究对象,针对边坡评价中常见的不确定性因素,可靠度分析是值得利用的方法。为评价某节理发育的岩质岸坡稳定性,通过有限元计算软件,结合现场勘探测绘数据,建立以边坡节理强度参数c、φ为输入变量,安全系数为输出变量的点估计(PEM)计算概率模型,计算结果表明:节理发育对该边坡变形具有明显控制作用;边坡整体可靠性较好,破坏概率极低。最后,通过蒙托卡罗法对可靠度结果进行验证,结果表明两种方法的计算结果不存在显著性差异。研究结果表明节理对岩质边坡稳定具有良好的敏感性,基于节理不确定性的点估计法分析边坡可靠度是一种有效的方法。
Abstract:Slope stability has always been the key research object of slope safety. In view of the common uncertain factors in slope evaluation, reliability analysis is a valuable method. To evaluate the stability of a jointed rock slope, a point estimation (PEM) calculation probability model is established by using the finite element analysis software and the field survey data, The PEM method takes the joint strength parameters c, φ and the safety factor as input and output variables. The results suggest that, the joints have a significant control effect on the deformation of the slope; The overall reliability of slope is great, and the failure probability is extremely low. Finally, the reliability results are verified by Monte Carlo method, and the results show that there is no significant difference between the two methods. The results indicate that the joints have good sensitivity to the stability of rock slope, and the point estimation method based on joint uncertainty is an effective method to analyze the slope reliability.
-
Key words:
- Jointed rock slope /
- reliability /
- baecher model /
- point estimate /
- Monte carlo
-

-
表 1 岩体参数取值
Table 1. Parameter values of rock mass
材料 弹性模量/MPa 泊松比 φ/(°) c/MPa 容重/(kN·m−3) 均值 标准差 均值 标准差 强风化花岗岩 10000 0.28 38 2 0.12 0.01 23.5 弱风化花岗岩 13000 0.26 42 2 0.15 0.02 25.0 微新花岗岩 20000 0.25 49 3 0.50 0.04 27.0 表 2 结构面几何特征值
Table 2. Geometric characteristc values of structural plane
边坡分层 节理组 产状 迹长 密度/(条·m−2) 平均倾向/(°) 平均倾角/(°) 分布类型 Fisher常数 均值/m 分布类型 强风化层 J1 235 67 Fisher 95 8 负指数分布 0.20 J2 125 45 45 5.5 0.25 J1 245 74 50 15 负指数分布 0.06 弱风化层 J2 125 58 Fisher 40 5 0.03 J3 105 30 90 5 0.05 微新基岩 J1 236 78 Fisher 30 6 负指数分布 0.02 J2 135 55 110 4 0.01 表 3 结构面强度特征值
Table 3. Strength characteristic values of structural plane
节理组号 φ/(°) c/MPa 法向刚度/(MPa·m−1) 切向刚度/(MPa·m−1) 抗拉强度/MPa 均值 标准差 均值 标准差 J1 30 2 0.04 0.002 8000 2500 0 J2 33 2 0.08 0.003 10000 3000 0 J3 38 3 0.10 0.005 13000 3800 0 表 4 敏感性计算结果
Table 4. Sensitivity calculation results
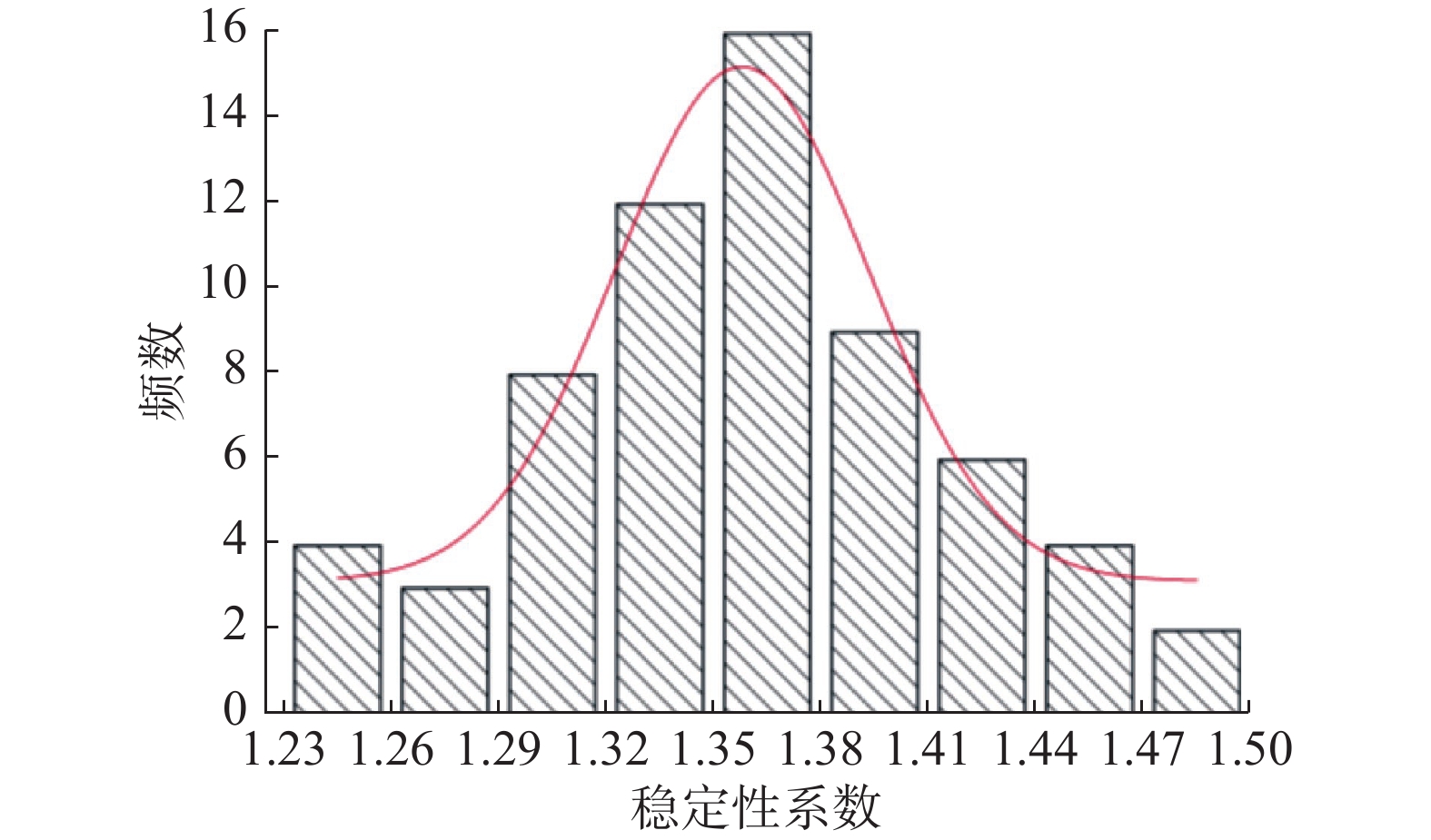
节理强度参数 岩体强度参数 稳定性系数 c/MP φ/(°) c/MPa φ/(°) 0.04 30 0.15 42 1.35 0.034 30 0.15 42 1.33 0.046 30 0.15 42 1.38 0.04 24 0.15 42 1.23 0.04 36 0.15 42 1.45 0.04 30 0.144 42 1.34 0.04 30 0.156 42 1.37 0.04 30 0.150 36 1.27 0.04 30 0.150 48 1.44 表 5 敏感性指标计算结果
Table 5. Sensitivity index calculation results
节理强度参数 岩体强度参数 c/MP φ/(°) c/MP φ/(°) 0.0370 0.1630 0.0222 0.1259 表 6 可靠度对比分析结果
Table 6. Results of reliability comparison analysis
稳定性参数 JEF-PEM点估计 MCS蒙托卡罗 平均值 1.344 1.590 标准差 0.0573 0.0854 可靠性指数 6.007 6.907 破坏概率 0.001 <0.001 -
[1] 陈祖煜, 陈立宏, 王玉杰, 等. 滑坡和建筑物抗滑稳定分析中的可靠度分析和分项系数设计方法[C]//陈祖煜. 水利水电工程风险分析及可靠度设计技术进展. 北京: 中国水利水电出版社, 2010: 27–39
CHEN Zuyu, CHEN Lihong, WANG Yujie, et al. Reliability analysis and partial factor design methods for slope stability[C]// CHEN Zuyu. Proceedings of the symposium on risk analysis and reliability based design for water resources and hydropower projects. Beijing: China Water Power Press, 2010: 27–39. (in Chinese)
[2] 刘超, 袁颖, 左朝晖, 等. 考虑土参数自相关距离影响的单桩可靠性设计方法[J]. 水文地质工程地质,2020,47(3):122 − 127. [LIU Chao, YUAN Ying, ZUO Zhaohui, et al. Pile reliability design considering the influence of soil auto-correlation distance[J]. Hydrogeology & Engineering Geology,2020,47(3):122 − 127. (in Chinese with English abstract)
[3] 李涛, 刘国栋, 王聪. 基于可靠度理论的尾矿坝失稳概率及敏感性分析[J]. 中国地质灾害与防治学报,2019,30(3):81 − 86. [LI Tao, LIU Guodong, WANG Cong. Instability probability and sensitivity analysis of tailings dam based on reliability theory[J]. The Chinese Journal of Geological Hazard and Control,2019,30(3):81 − 86. (in Chinese with English abstract)
[4] JIANG S H, LI D Q, ZHANG L M, et al. Slope reliability analysis considering spatially variable shear strength parameters using a non-intrusive stochastic finite element method[J]. Engineering Geology,2014,168:120 − 128. doi: 10.1016/j.enggeo.2013.11.006
[5] LI Y J, HICKS M A, NUTTALL J D. Comparative analyses of slope reliability in 3D[J]. Engineering Geology,2015,196:12 − 23. doi: 10.1016/j.enggeo.2015.06.012
[6] ZHAO L H, YU C H, CHENG X, et al. A method for seismic stability analysis of jointed rock slopes using Barton-Bandis failure criterion[J]. International Journal of Rock Mechanics and Mining Sciences,2020,136:104487. doi: 10.1016/j.ijrmms.2020.104487
[7] LU R L, WEI W, SHANG K W, et al. Stability analysis of jointed rock slope by strength reduction technique considering ubiquitous joint model[J]. Advances in Civil Engineering,2020,2020:8862243.
[8] 冯开帅, 姜谙男, 吴洪涛, 等. 顺层非贯通节理边坡稳定性及破坏模式研究[J]. 公路工程,2020,45(6):52 − 58. [FENG Kaishuai, JIANG Annan, WU Hongtao, et al. Study on failure mode and stability of slope based on intermittent joints[J]. Highway Engineering,2020,45(6):52 − 58. (in Chinese with English abstract)
[9] CHANG Y, CHANG L S, REN F Q. Strength anisotropy of jointed rock slope considering mining damage: A numerical analysis method[J]. Geomatics, Natural Hazards and Risk,2020,11(1):2587 − 2614. doi: 10.1080/19475705.2020.1856200
[10] 陈国良, 廖国华. 岩体节理网络的计算机模拟[J]. 有色金属(矿山部分),1989,41(6):23 − 28. [CHEN Guoliang, LIAO Guohua. Computer simulation of rock mass joint network[J]. Nonferrous Metals (Mining),1989,41(6):23 − 28. (in Chinese)
[11] 王宏, 陶振宇. 边坡稳定分析的节理网络模拟原理及工程应用[J]. 水利学报,1993,24(10):20 − 27. [WANG Hong, TAO Zhenyu. The principle of joint network simulation in the stability analysis of rock slope and its engineering application[J]. Journal of Hydraulic Engineering,1993,24(10):20 − 27. (in Chinese with English abstract) doi: 10.3321/j.issn:0559-9350.1993.10.003
[12] 严豪, 宋彦辉, 陈子玉. 基于Voronoi节理模型的碎裂岩边坡稳定性分析[J]. 中国地质灾害与防治学报,2018,29(1):34 − 39. [YAN Hao, SONG Yanhui, CHEN Ziyu. Stability analysis of broken rock slope based on Voronoi joint net model[J]. The Chinese Journal of Geological Hazard and Control,2018,29(1):34 − 39. (in Chinese with English abstract)
[13] 李源亮, 任光明, 刘艳领, 等. 基于节理网络有限元的岩质边坡稳定性分析[J]. 长江科学院院报,2019,36(1):78 − 83. [LI Yuanliang, REN Guangming, LIU Yanling, et al. Stability analysis of rock slope based on finite elements with joint network[J]. Journal of Yangtze River Scientific Research Institute,2019,36(1):78 − 83. (in Chinese with English abstract) doi: 10.11988/ckyyb.20170823
[14] 肖术, 吴顺川, 高永涛, 等. 基于PEM-JFEM方法的节理岩质边坡稳定性评价[J]. 工程科学学报,2015,37(7):844 − 850. [XIAO Shu, WU Shunchuan, GAO Yongtao, et al. Jointed rock slope stability evaluation based on PEM- JFEM method[J]. Chinese Journal of Engineering,2015,37(7):844 − 850. (in Chinese with English abstract)
[15] 张宜杰, 任光明, 常文娟, 等. 节理岩质边坡稳定性概率分析[J]. 成都理工大学学报(自然科学版),2021,48(2):235 − 241. [ZHANG Yijie, REN Guangming, CHANG Wenjuan, et al. Probabilistic analysis of stability of jointed rock slope[J]. Journal of Chengdu University of Technology (Science & Technology Edition),2021,48(2):235 − 241. (in Chinese with English abstract)
[16] PRZEWLOCKI J, ZABUSKI L, WINKELMANN K. Reliability analysis of sea cliff slope stability by point estimate method[J]. IOP Conference Series:Materials Science and Engineering,2019,471:042003. doi: 10.1088/1757-899X/471/4/042003
[17] 许湘华, 曲广琇, 方理刚. 基于节理几何参数不确定性的边坡可靠度分析[J]. 中南大学学报(自然科学版),2010,41(3):1139 − 1145. [XU Xianghua, QU Guangxiu, FANG Ligang. Reliability analysis of rock slope based on uncertainty of joint geometric parameters[J]. Journal of Central South University (Science and Technology),2010,41(3):1139 − 1145. (in Chinese with English abstract)
[18] 王双, 陈征宙, 吴强, 等. 基于节理产状不确定性的边坡稳定性及敏感度分析[J]. 岩土工程学报,2013,35(2):348 − 354. [WANG Shuang, CHEN Zhengzhou, WU Qiang, et al. Stability and sensitivity analysis of slopes based on uncertainty of joint orientations[J]. Chinese Journal of Geotechnical Engineering,2013,35(2):348 − 354. (in Chinese with English abstract)
[19] 王双. 节理产状概率模型研究及其在产状分组和岩坡不确定分析中的应用[D]. 南京: 南京大学, 2013
WANG Shuang. Research on distribution model of joint orientations and its application to joint set clustering and rock slope uncertainty analysis[D]. Nanjing: Nanjing University, 2013. (in Chinese with English abstract)
[20] 申矫健. 基于参数不确定性的岩质边坡稳定性分析方法研究[D]. 赣州: 江西理工大学, 2014
SHEN Jiaojian. Study on stability analysis method of rock slope based on parameter uncertainty[D]. Ganzhou: Jiangxi University of Science and Technology, 2014. (in Chinese with English abstract)
[21] BAECHER G B, LANNEY N A, EINSTEIN H H. Statistical description of rock properties and sampling[J]. 18th U S Symposium on Rock Mechanics, USRMS 1977,1977:5 − 8.
[22] 王宇, 李晓, 刘帅, 等. 岩体离散裂隙网络稳定性计算的节理有限元法[J]. 岩石力学与工程学报,2013,32(增刊 2):3337 − 3345. [WANG Yu, LI Xiao, LIU Shuai, et al. Stability calculation for discrete fracture network of rock masses based on joint finite element method[J]. Chinese Journal of Rock Mechanics and Engineering,2013,32(Sup 2):3337 − 3345. (in Chinese with English abstract)
[23] CACAS M C, LEDOUX E, DE MARSILY G, et al. Modeling fracture flow with a stochastic discrete fracture network: calibration and validation: 1. The flow model[J]. Water Resources Research,1990,26(3):479 − 489.
[24] DERSHOWITZ W S, EINSTEIN H H. Characterizing rock joint geometry with joint system models[J]. Rock Mechanics and Rock Engineering,1988,21(1):21 − 51. doi: 10.1007/BF01019674
[25] ROSENBLUETH E. Point estimates for probability moments[J]. Proceedings of the National Academy of Sciences of the United States of America,1975,72(10):3812 − 3814. doi: 10.1073/pnas.72.10.3812
[26] 李侃, 巨能攀. 基于蒙特卡洛方法的边坡可靠性评价[J]. 中国地质灾害与防治学报,2014,25(1):23 − 27. [LI Kan, JU Nengpan. Integrated application of Monte-Carlo simulation for landslide reliability analysis[J]. The Chinese Journal of Geological Hazard and Control,2014,25(1):23 − 27. (in Chinese with English abstract)
-




 下载:
下载: