Assessment of exceedance probability of landslide run-out distance and hazard zoning
-
摘要:
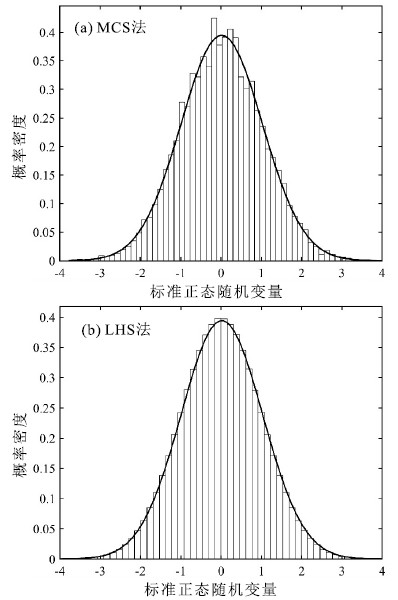
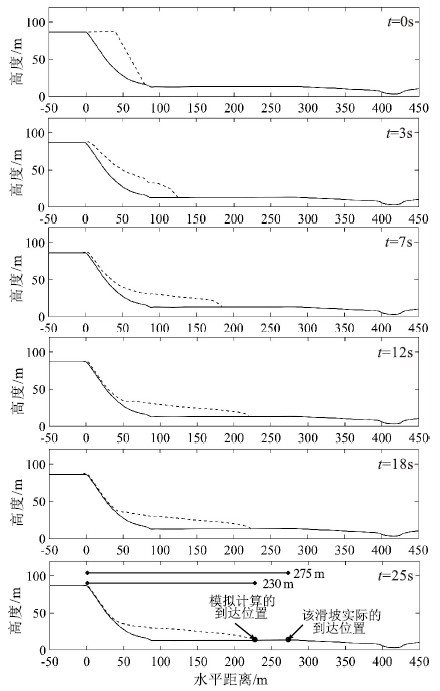
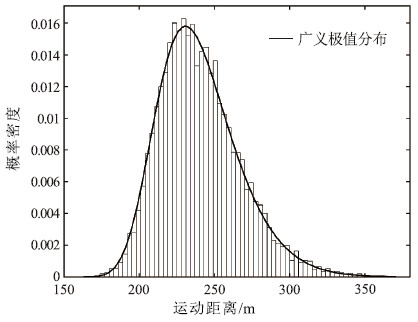
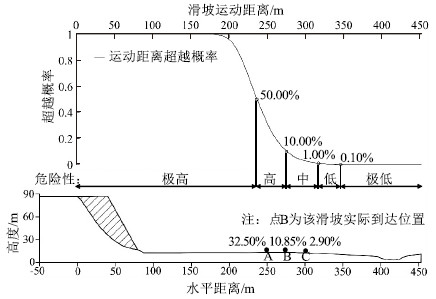
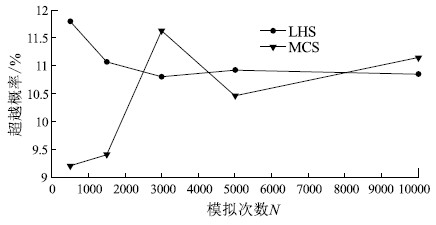
针对岩土体物理力学参数不确定性强、动态数值模拟方法对滑坡运动距离预测精度有限的问题,提出一种基于拉丁超立方采样法(LHS)的滑坡运动距离超越概率定量评价方法,以提高滑坡滑程预测结果的可靠性。该方法将滑坡计算参数考虑为服从某种概率分布的随机变量,使用LHS对随机变量进行分层抽样,并基于动态数值模型计算每组随机样本对应的滑坡运动距离,最后,通过构建不同运动距离阈值下的极限状态函数计算运动距离超越某一给定位置的概率。应用该方法对大堡子滑坡运动距离进行评价,得到该滑坡运动距离在95%置信水平下的置信区间为[196 m,302 m];并根据运动距离-超越概率图,提出以50%、10%、1%和0.1%作为分界概率值将该滑坡潜在威胁范围分为极高、高、中、低、极低5个危险性等级。计算结果显示,滑坡实际运动距离在95%置信区间内,实际的威胁范围也在划分的高-极高危险区内,说明评价结果合理,证明了基于运动距离超越概率的滑坡运动危险性评价的有效性。研究成果为滑坡运动距离评价及危险性区划提供了新的思路,具有重要的理论意义和工程实用价值。
Abstract:In view of the large uncertainties embedded in the physical and mechanical parameters of the dynamic numerical model, a quantitative method to assess exceedance probability of landslide run-out distance based on Latin Hypercube Sampling(LHS) is proposed to improve the reliability of landslide slide prediction results.In the proposed method, the input parameters are considered as random variables with probability distribution functions; the LHS is used to generate stratified samplings for the random variables, and the dynamic numerical model is used to compute the landslide run-out distance corresponding to each random sample; and finally, the exceedance probability of landslide run-out distance is calculated by constructing limit state functions for different run-out distance threshold values.The proposed method is applied to conduct a probabilistic assessment of the run-out distance for Dabaozi landslide, and the 95% confidence interval of the run-out distance is computed as[196 m, 302 m].According to the run-out distance-exceedance probability curve, the potential affected area of the landslide is classified into five categories(i.e., extremely high, high, medium, low and extremely low) based on different threshold values of exceedance probability(i.e., 50%, 10%, 1% and 0.1%).The calculation results show that the actual run-out distance of landslide is within the 95% confidence interval, and the actual threat range is also within the classified high-extremely high danger zone.The results show that the evaluation results are reasonable and the landslide movement risk evaluation based on the distance exceeding probability is also proved effective.The proposed method may provide new ideas for landslide run-out distance assessment and for hazard zoning, which has important theoretical significance and practical engineering value.
-
Key words:
- landslide run-out distance /
- dynamic numerical model /
- LHS /
- exceedance probability /
- hazard zoning
-

-
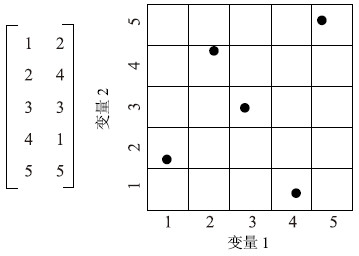
图 1 拉丁超立方采样(2个随机变量,5次模拟)[25]
Figure 1.
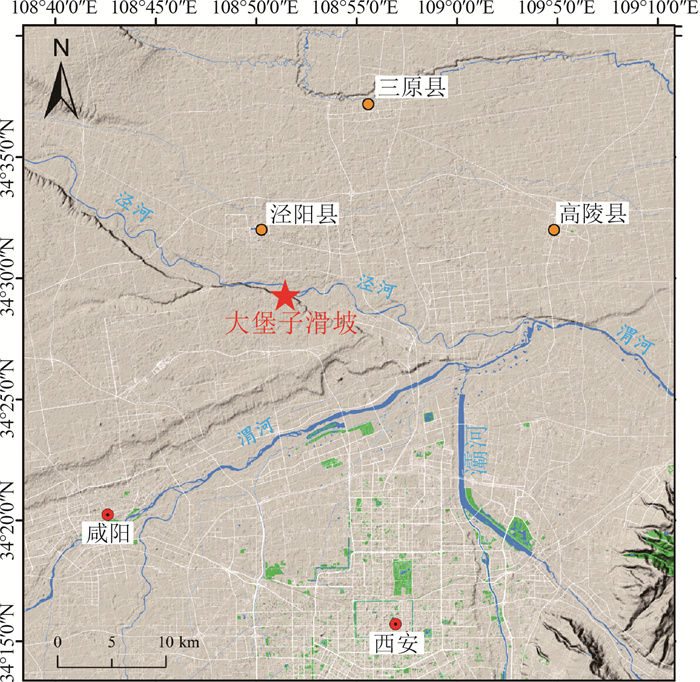
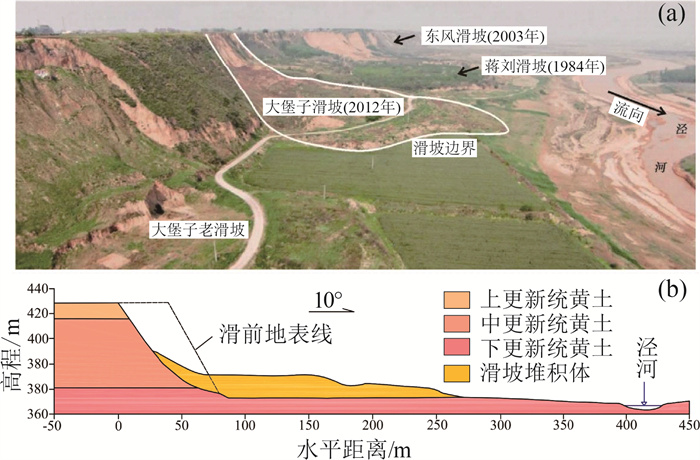
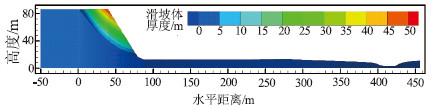
图 5 大堡子滑坡全貌图(a)与剖面(b)[27]
Figure 5.
表 1 土体参数的变异性级别[29]
Table 1. ariability classification of soil parameters
变异系数 δ≤0.1 0.1δ≤0.2 0.2δ≤0.3 0.3δ≤0.4 δ>0.4 变异性 很低 低 中等 高 很高 表 2 随机变量的统计特征
Table 2. Statistical characteristics of random variables
随机变量 ρ
/(kg·m-3)c′
/kPaφ′
/°ru 均值 1800 39 25 0.65 变异系数 0.05 0.3 0.15 - 参数范围 [0, +∞) [0, +∞) [0, +∞) [0.5, 0.8] 分布类型 对数正态 对数正态 对数正态 均匀 表 3 事件可能性分类[33]
Table 3. Event likelihood classification
不确定性 描述 概率值/% 几乎
确定由已知物理条件或过程,事件几乎确定发生 99.9 非常
可能事件极有可能发生,但也可能不会发生,如果没有发生,人们会感到惊讶 99 可能 事情是可能发生的,但不一定发生 90 完全不确定 没有理由相信一种结果比另一种结果更可能或更不可能发生 50 不可能 事件不太可能发生,但它有可能发生 10 非常不可能 不能根据已知的物理条件或其他原因完全排除事件发生的可能性 1 几乎不可能 由已知的物理条件或过程,事件几乎不可能发生 0.1 -
[1] Dai F C, Lee C F, Ngai Y Y. Landslide risk assessment and management: an overview[J]. Engineering Geology, 2002, 64(1): 65-87. doi: 10.1016/S0013-7952(01)00093-X
[2] 吴越, 刘东升, 周忠浩. 考虑滑动过程内部崩解耗散的滑坡体运动模型[J]. 岩土工程学报, 2015, 37(1): 35-46. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201501004.htm
[3] Corominas J, van Westen C, Frattini P, et al. Recommendations for the quantitative analysis of landslide risk[J]. Bulletin of Engineering Geology and the Environment, 2014, 73(2): 209-263. http://core.ac.uk/download/pdf/38629048.pdf
[4] 詹威威, 黄润秋, 裴向军, 等. 沟道型滑坡-碎屑流运动距离经验预测模型研究[J]. 工程地质学报, 2017, 25(1): 154-163. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201701021.htm
[5] 邵葆蓉, 孙即超, 朱月琴, 等. 基于多元回归的黄土滑坡滑动距离预测模型探讨——以甘肃天水地区为例[J]. 地质通报, 2020, 39(12): 1993-2003. http://dzhtb.cgs.cn/gbc/ch/reader/view_abstract.aspx?file_no=20201213&flag=1
[6] Zhan W, Fan X, Huang R, et al. Empirical prediction for travel distance of channelized rock avalanches in the Wenchuan earthquake area[J]. Natural Hazards & Earth System Sciences, 2017, 17(6): 833-844. http://www.ingentaconnect.com/content/doaj/15618633/2017/00000017/00000001/art00012
[7] Hungr O, McDougall S. Two numerical models for landslide dynamic analysis[J]. Computers & Geosciences, 2009, 35(5): 978-992. http://www.sciencedirect.com/science?_ob=ShoppingCartURL&_method=add&_eid=1-s2.0-S0098300408000289&originContentFamily=serial&_origin=article&_ts=1490054550&md5=89f93acdf526fbdab24cf890094345a2
[8] Beguería S, Van Asch T W J, Malet J P, et al. A GIS-based numerical model for simulating the kinematics of mud and debris flows over complex terrain[J]. Natural Hazards and Earth System Sciences, 2009, 9(6): 1897-1909. doi: 10.5194/nhess-9-1897-2009
[9] Christen M, Kowalski J, Bartelt P. RAMMS: Numerical simulation of dense snow avalanches in three-dimensional terrain[J]. Cold Regions Science and Technology, 2010, 63(1/2): 1-14. http://www.onacademic.com/detail/journal_1000035369102510_59d8.html
[10] Van Westen C J, Van Asch T W J, Soeters R. Landslide hazard and risk zonation-why is it still so difficult?[J]. Bulletin of Engineering Geology and the Environment, 2006, 65(2): 167-184. doi: 10.1007/s10064-005-0023-0
[11] Quan L. Dynamic numerical run-out modeling for quantitative landslide risk assessment[D]. Doctoral Thesis of University of Twente, ITC, 2012, 206: 1-237.
[12] Luna B Q, Cepeda J, Stumpf A, et al. Application of a Monte Carlo method for modeling debris flow run-out[C]//EGU General Assembly Conference. EGU General Assembly Conference Abstracts, 2012.
[13] 祝玉学. 边坡可靠性分析[M]. 北京: 冶金工业出版, 1993.
[14] Zahra T. Quantifying uncertainties in Landslide Runout Modelling[M]. University of Twente Faculty of Geo-Information and Earth Observation(ITC), 2010.
[15] Zaalishvili V B, Rogozhin E A. Assessment of seismic hazard of territory on basis of modern methods of detailed zoning and seismic microzonation[J]. Open Construction and Building Technology Journal, 2011, 5: 30-40.
[16] 唐荣昌, 张耀国, 黄祖智, 等. 四川石棉-西昌地区地震区划研究[J]. 地震研究, 1993, 16(3): 306-315. https://www.cnki.com.cn/Article/CJFDTOTAL-DZYJ199303011.htm
[17] 唐川, 周钜乾, 朱静, 等. 泥石流堆积扇危险度分区评价的数值模拟研究[J]. 灾害学, 1994, 9(4): 7-13. https://www.cnki.com.cn/Article/CJFDTOTAL-ZHXU404.001.htm
[18] Wei F, Hu K, Lopez J L, et al. Method and its application of the momentum model for debris flow risk zoning[J]. Chinese Science Bulletin, 2003, 48(6): 594. doi: 10.1360/03tb9126
[19] Ouyang C, He S, Xu Q, et al. A MacCormack-TVD finite difference method to simulate the mass flow in mountainous terrain with variable computational domain[J]. Computers & Geosciences, 2013, 52: 1-10. http://or.nsfc.gov.cn/bitstream/00001903-5/57006/1/1000007119136.pdf
[20] Ouyang C, He S, Tang C. Numerical analysis of dynamics of debris flow over erodible beds in Wenchuan earthquake-induced area[J]. Engineering Geology, 2015, 194: 62-72. doi: 10.1016/j.enggeo.2014.07.012
[21] Ouyang C, He S, Xu Q. MacCormack-TVD finite difference solution for dam break hydraulics over erodible sediment beds[J]. Journal of Hydraulic Engineering, 2014, 141(5): 06014026.
[22] Ouyang C, Zhao W, He S, et al. Numerical modeling and dynamic analysis of the 2017 Xinmo landslide in Maoxian County, China[J]. Journal of Mountain Science, 2017, 14(9): 1701-1711. doi: 10.1007/s11629-017-4613-7
[23] Xing A G, Wang G, Yin Y P, et al. Dynamic analysis and field investigation of a fluidized landslide in Guanling, Guizhou, China[J]. Engineering Geology, 2014, 181: 1-14. doi: 10.1016/j.enggeo.2014.07.022
[24] McKay M D, Beckman R J, Conover W J. Comparison of three methods for selecting values of input variables in the analysis of output from a computer code[J]. Technometrics, 1979, 21(2): 239-245. http://r-forge.r-project.org/scm/viewvc.php/*checkout*/doc/McKay1979.pdf?root=lhs
[25] Olsson A, Sandberg G, Dahlblom O. On Latin hypercube sampling for structural reliability analysis[J]. Structural Safety, 2003, 25(1): 47-68. doi: 10.1016/S0167-4730(02)00039-5
[26] 吴振君. 土体参数空间变异性模拟和土坡可靠度分析方法应用研究[D]. 中国科学院研究生院(武汉岩土力学研究所)博士学位论文, 2009.
[27] 沈伟, 翟张辉, 李同录, 等. 陕西泾河南岸大堡子高速远程黄土滑坡运动过程模拟[J]. 工程地质学报, 2016, 24(6): 1309-1317. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201606034.htm
[28] 郭剑. 一种双层结构的高速远程滑坡运动学模型及应用[D]. 长安大学硕士学位论文, 2018.
[29] 重庆市质量技术监督局. DB50/T 143-2018地质灾害防治工程勘查规范[S]. 2018.
[30] 袁晓蕾. 黄土滑坡的滑带土强度试验参数统计及可靠性研究[D]. 长安大学硕士学位论文, 2007.
[31] 倪万魁, 韩启龙. 黄土土性参数的统计分析[J]. 工程地质学报, 2001, 9(1): 62-67. doi: 10.3969/j.issn.1004-9665.2001.01.011
[32] Gao Y, Yin Y, Li B, et al. Investigation and dynamicanalysis of the long runout catastrophic landslide at the Shenzhen landfill on December 20, 2015, in Guangdong, China[J]. Environmental Earth Sciences, 2017, 76(1): 13. doi: 10.1007/s12665-016-6332-8
[33] Lacasse S, Nadim F. Learning to live with geohazards: from research to practice[M]. Geo-Risk 2011: Risk Assessment and Management, 2011: 64-116.
-



 下载:
下载: