Inversion of hydraulic parameters of high permeability confined aquifer based on slug test
-
摘要:
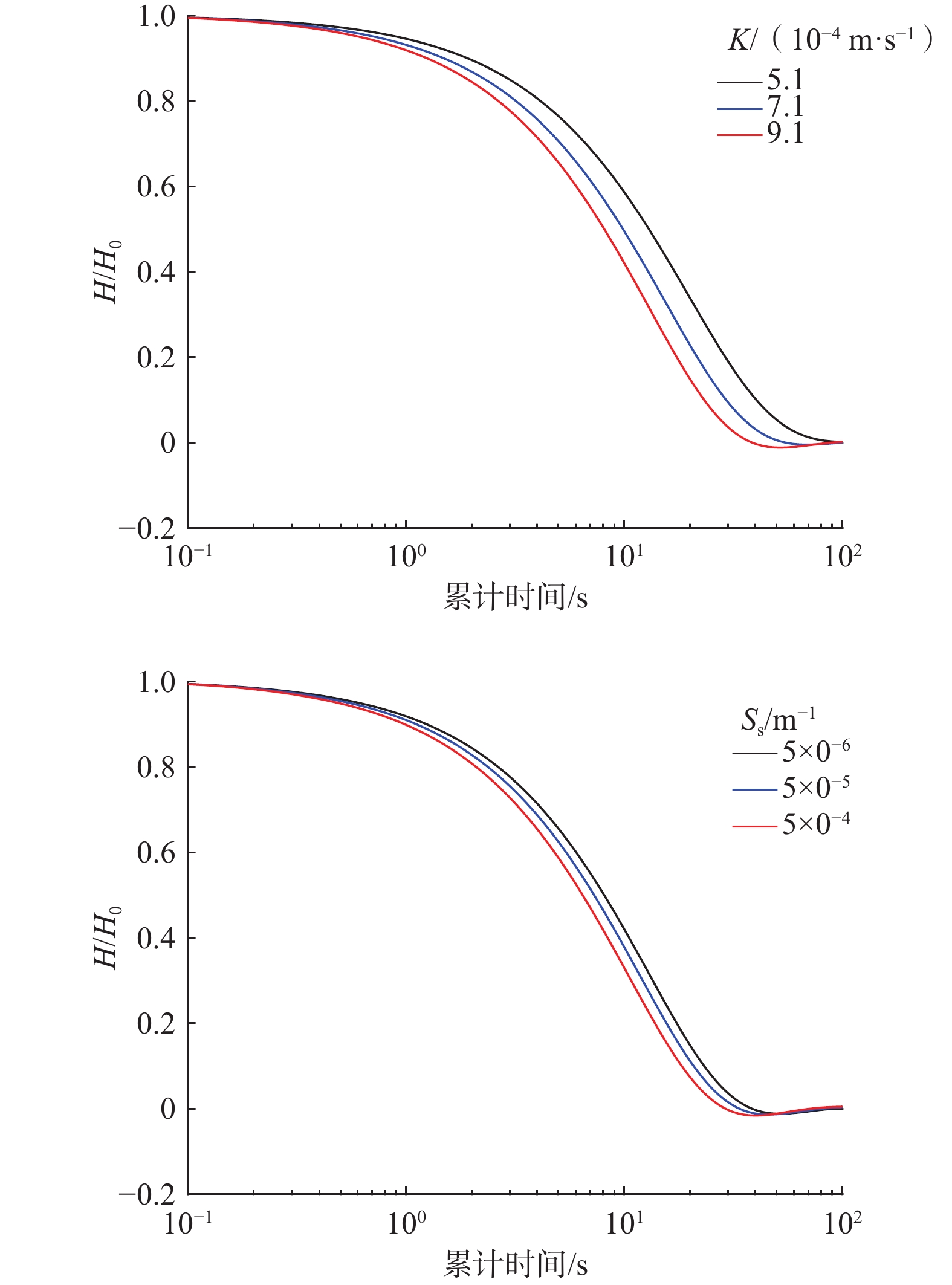
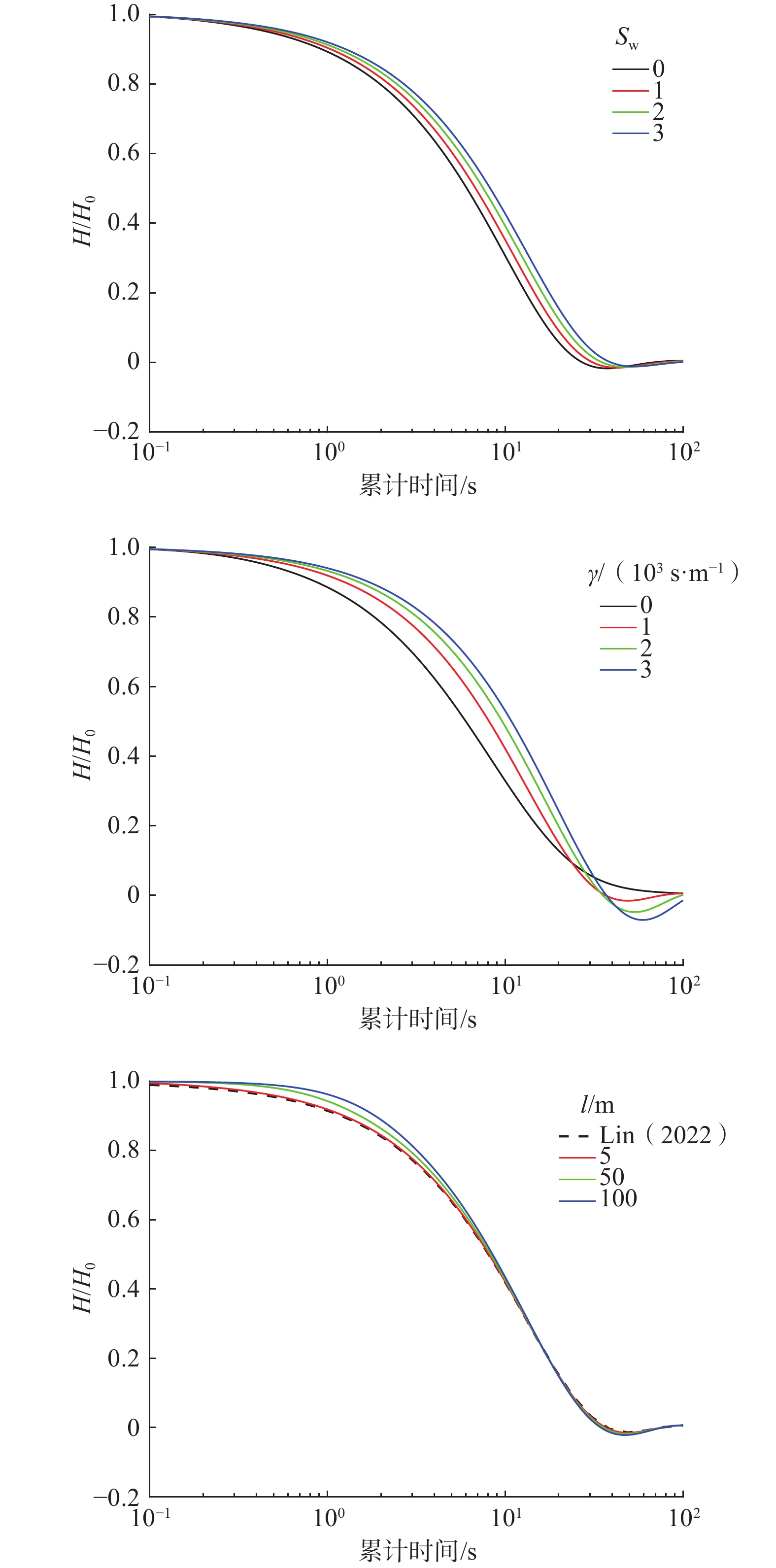
为了提高高渗透性承压含水层渗透系数与储水率等水文地质参数的反演精度,科学解释井筒水位的非线性振荡现象,本研究建立了考虑表皮效应和非达西流效应耦合惯性力作用的微水试验模型。模型中表皮效应采用Robbin边界条件描述,非达西流效应采用Forchheimer方程刻画,惯性力作用采用动量平衡方程表达。利用Laplace变换法推导模型的解析解,基于现场试验数据,分析3种因素对反演水文地质参数的影响。结果表明表皮效应、非达西流效应与惯性力作用对参数反演结果的影响均不能忽视。无因次表皮因子$ ({S}_{\mathrm{w}}) $值、Forchheimer系数$ (\gamma ) $值与瞬时注水后井筒水位与承压含水层隔水顶板之间的垂直距离$ (l) $3个值越大,井筒水位恢复速度越慢;$ {S}_{\mathrm{w}} $值越大,井筒水位振荡幅度越小,而$ \gamma $值和$ l $值越大,井筒水位振荡幅度越大。忽略表皮效应、非达西流效应或惯性力作用均导致渗透系数与储水率的反演结果偏小。研究结果为裂隙承压含水层中水文地质参数的反演提供了一种合理的理论基础和技术依据。
Abstract:To improve the accuracy of estimated hydraulic parameters such as hydraulic conductivity and specific storage in confined aquifers with high permeability, and provide a scientific explanation for the nonlinear oscillation phenomenon of test well water levels, this study established a slug test model that takes into account the skin and non-Darcy flow effects, as well as inertial force action. The skin effect was described by Robbin boundary conditions and the non-Darcy flow effect was explained by the Forchheimer equation; momentum balance equation expressed the inertial force action . The Laplace transform method was used to derive the analytical solution of this model. Then the impacts of three factors on estimating of hydraulic parameters were analyzed using field data. The results show that the influences of skin effect, non-Darcy flow effect, and inertia force action on the parameter estimation cannot be ignored. More specifically, the higher values of the dimensionless skin factor (Sw), the Forchheimer coefficient (γ), and the vertical distance (l) between the water level in the well and the top of the confined aquifer after instantaneous water injection, the slower rate of water level recovery. As the value of Sw increases, the amplitude of water level oscillation decreases, whereas the amplitudes of water level oscillation increase with larger values of γ and l. Ignoring the skin effect, non-Darcy flow effect or inertia force will lead to underestimating hydraulic conductivity and specific storage. The results can provide theoretical guidance and technical support for the inversion of hydraulic parameters in fractured confined aquifers.
-
Key words:
- slug tests /
- skin effect /
- non-Darcian flow /
- inertial force action /
- hydraulic conductivity /
- specific storage
-

-
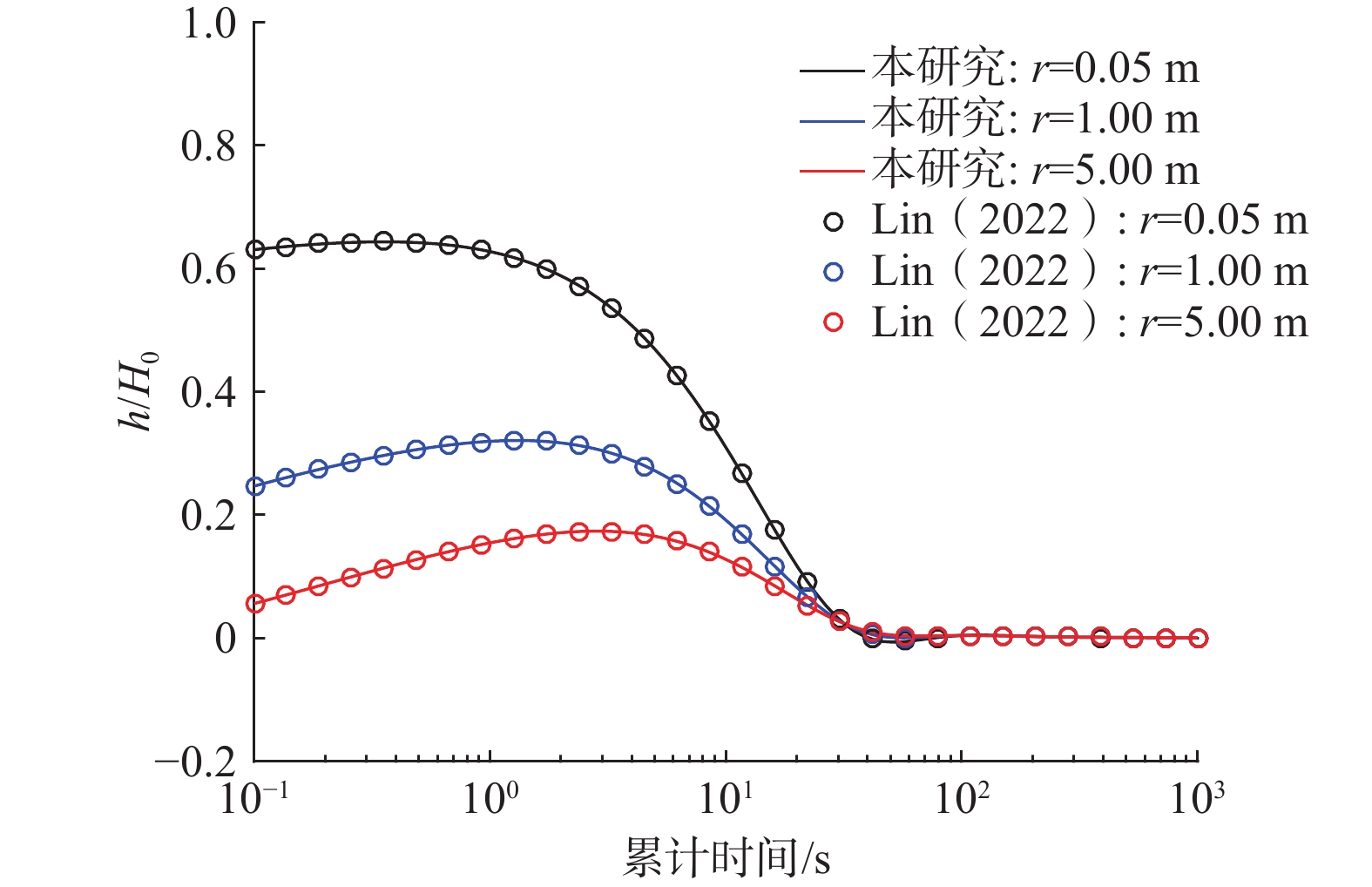
图 2 本研究模型和Lin等[20]在不同
$ r $ 处的水位恢复对比Figure 2.
表 1 模型参数
Table 1. Parameters used in this study
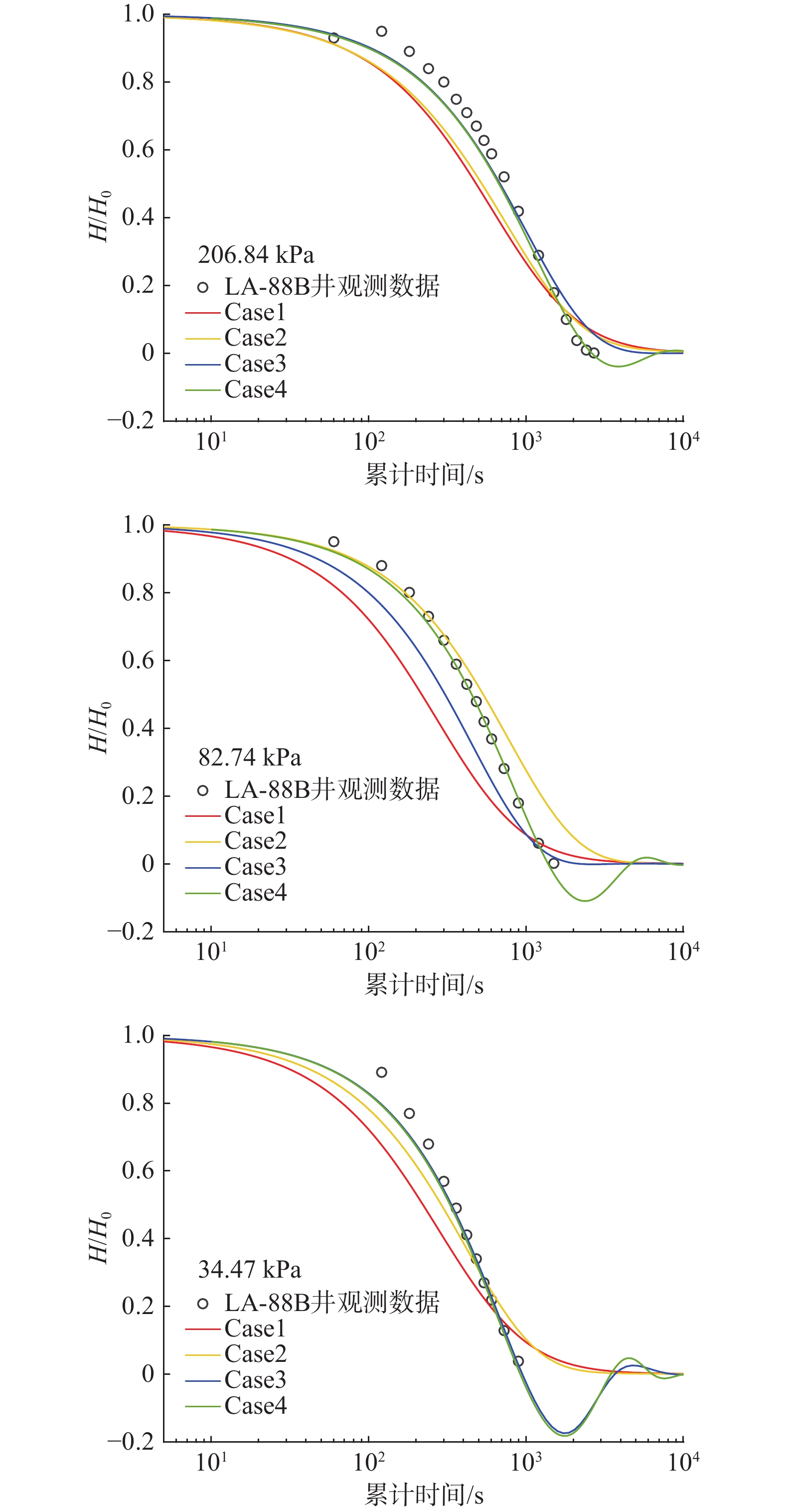
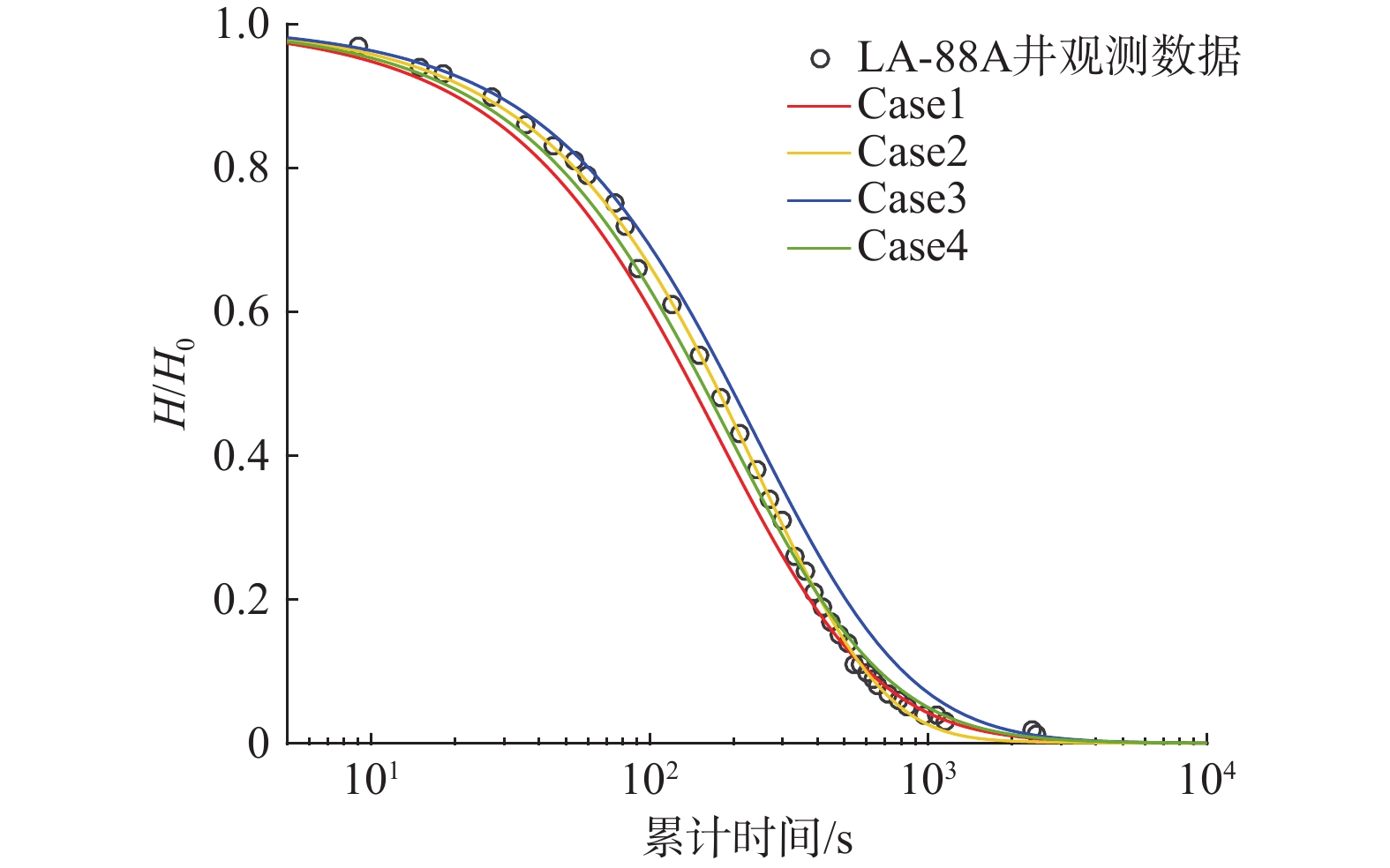
参数 取值 承压含水层厚度 $ /\mathrm{m} $ 1.5 井筒初始水位位移 $ /\mathrm{m} $ 0.35 储水率/m−1 5.0×10−6 渗透系数/(m·s−1) 9.1×10−4 连接管管径/m 5.0×10−2 井筒井径/m 5.0×10−2 无因次表皮因子 2.8 Forchheimer 系数/(s·m−1) 1.0×103 重力加速度/(m·s−2) 9.8 地下水运动黏滞系数/(m2·s−1) 1.2×10−6 瞬时注水后井筒水位与承压含水层隔水顶板之间的垂直距离/m 5.0 表 2 LA-87B、LA-88B、LA-88A井参数估计
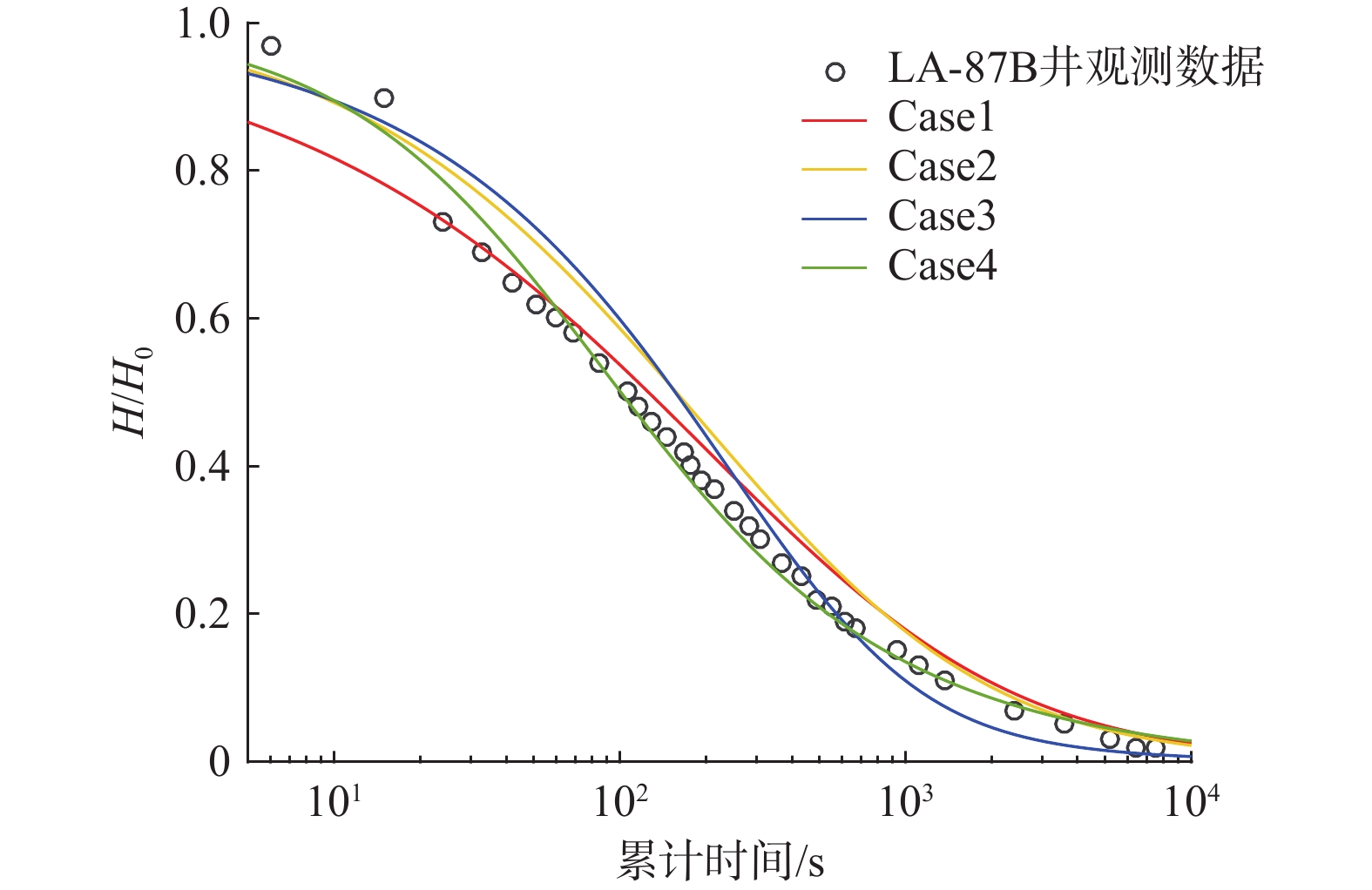
Table 2. Parameter estimation for wells LA-87B, LA-88B, and LA-88A
K/(m·s−1) Ss/s−1 Sw γ/(s·m−1) l/m 均方根误差 LA-87B, pa = 44.81 kPa Case 1 2.38×10−8 5.20×10−3 − 1.49×102 10 4.50×10−2 Case 2 2.72×10−8 5.20×10−3 0.10 − 10 6.21×10−2 Case 3 9.32×10−8 4.65×10−2 0.09 1.49×102 − 6.01×10−2 Case 4 1.19×10−8 4.65×10−2 0.07 1.49×102 10 2.30×10−2 LA-88B, pa = 206.84 kPa Case 1 1.48×10−7 4.08×10−10 − 4.07×105 10 1.21×10−1 Case 2 1.46×10−7 4.65×10−10 0.10 − 10 1.04×10−2 Case 3 6.25×10−7 6.69×10−11 34.80 4.07×105 − 5.09×10−2 Case 4 1.38×10−7 6.95×10−7 1.67 4.07×106 10 4.39×10−2 LA-88B, pa = 82.74 kPa Case 1 2.26×10−7 1.10×10−10 − 2.63×105 10 1.96×10−1 Case 2 1.10×10−6 1.10×10−9 59.70 − 10 8.37×10−2 Case 3 1.52×10−6 1.70×10−10 59.70 2.63×105 − 1.18×10−1 Case 4 2.17×10−6 3.67×10−10 49.70 4.07×105 10 1.91×10−2 LA-88B, pa = 34.47 kPa Case 1 3.24×10−7 2.87×10−10 − 7.70×104 10 1.37×10−1 Case 2 7.74×10−7 3.03×10−7 20.30 − 10 8.24×10−2 Case 3 1.93×10−6 4.25×10−10 11.45 7.70×106 − 3.99×10−2 Case 4 3.24×10−6 3.94×10−10 28.45 7.70×106 10 4.38×10−2 LA-88A, pa = 34.47 kPa Case 1 5.54×10−7 5.54×10−11 − 9.13×101 10 3.42×10−2 Case 2 1.34×10−6 4.16×10−8 19.90 − 10 9.10×10−3 Case 3 5.27×10−7 5.12×10−11 0.41 9.13×101 − 4.37×10−2 Case 4 5.27×10−7 5.12×10−11 0.41 9.13×101 10 2.05×10−2 -
[1] LIN Jingjing,MA Rui,SUN Ziyong,et al. Assessing the connectivity of a regional fractured aquifer based on a hydraulic conductivity field reversed by multi-well pumping tests and numerical groundwater flow modeling[J]. Journal of Earth Science,2023,34(6):1926 − 1939. doi: 10.1007/s12583-022-1674-5
[2] 吴延浩,江思珉,吴自军. 地下水污染强度及渗透系数场的反演识别研究[J]. 水文地质工程地质,2023,50(4):193 − 203. [WU Yanhao,JIANG Simin,WU Zijun. Identification of groundwater pollution intensity and hydraulic conductivity field[J]. Hydrogeology & Engineering Geology,2023,50(4):193 − 203. (in Chinese with English abstract)]
WU Yanhao, JIANG Simin, WU Zijun. Identification of groundwater pollution intensity and hydraulic conductivity field[J]. Hydrogeology & Engineering Geology, 2023, 50(4): 193 − 203. (in Chinese with English abstract)
[3] MARIOS C K. Assessment of porous aquifer hydrogeological parameters using automated groundwater level measurements in Greece[J]. Journal of Groundwater Science and Engineering,2021,9(4):269 − 278.
[4] 张俊, 刘天罡, 董佳秋, 等. 含水层层状非均质对地下水流系统的影响[J]. 中国地质,2020,47(6):1715 − 1725. [ZHANG Jun, LIU Tiangang, DONG Jiaqiu, WANG Xiaoyong, ZHA Yuanyuan, TANG Xiaoping, YIN Lihe, Andrew J. Love. The impact of aquifer layered heterogeneity on groundwater flow system[J]. Geology in China,2020,47(6):1715 − 1725. (in Chinese with English abstract)]
ZHANG Jun, LIU Tiangang, DONG Jiaqiu, WANG Xiaoyong, ZHA Yuanyuan, TANG Xiaoping, YIN Lihe, Andrew J. Love. The impact of aquifer layered heterogeneity on groundwater flow system[J]. Geology in China, 2020, 47(6): 1715 − 1725. (in Chinese with English abstract)
[5] 王旭东,韩鹏飞,张锁,等. 基于HYDRUS模拟的ABCD模型变量及参数物理基础研究[J]. 水文地质工程地质,2023,50(5):20 − 27. [WANG Xudong,HAN Pengfei,ZHANG Suo,et al. Research on the physical basis of variables and parameters of ABCD model based on HYDRUS simulation[J]. Hydrogeology & Engineering Geology,2023,50(5):20 − 27. (in Chinese with English abstract)]
WANG Xudong, HAN Pengfei, ZHANG Suo, et al. Research on the physical basis of variables and parameters of ABCD model based on HYDRUS simulation[J]. Hydrogeology & Engineering Geology, 2023, 50(5): 20 − 27. (in Chinese with English abstract)
[6] 万伟锋,李清波,蔡金龙,等. 多孔均质含水层中激发强度对微水试验结果的影响[J]. 水文地质工程地质,2018,45(6):1 − 6. [WAN Weifeng,LI Qingbo,CAI Jinlong,et al. Research on the influence of the excitation intensity on slug test results in a homogeneous porous aquifer[J]. Hydrogeology & Engineering Geology,2018,45(6):1 − 6. (in Chinese with English abstract)]
WAN Weifeng, LI Qingbo, CAI Jinlong, et al. Research on the influence of the excitation intensity on slug test results in a homogeneous porous aquifer[J]. Hydrogeology & Engineering Geology, 2018, 45(6): 1 − 6. (in Chinese with English abstract)
[7] KIPP K L J. Type curve analysis of inertial effects in the response of a well to a slug test[J]. Water Resources Research,1985,21(9):1397 − 1408. doi: 10.1029/WR021i009p01397
[8] 刘颖,邵景力. 双重孔隙介质微水试验模型在倾斜裂隙含水层中的应用[J]. 水文地质工程地质,2016,43(2):1 − 8. [LIU Ying,SHAO Jingli. Application of a slug test model in the double porosity media to a sloping fractured formation[J]. Hydrogeology & Engineering Geology,2016,43(2):1 − 8. (in Chinese with English abstract)]
LIU Ying, SHAO Jingli. Application of a slug test model in the double porosity media to a sloping fractured formation[J]. Hydrogeology & Engineering Geology, 2016, 43(2): 1 − 8. (in Chinese with English abstract)
[9] WANG Quanrong,ZHAN Hongbin,WANG Yanxin. Non-Darcian effect on slug test in a leaky confined aquifer[J]. Journal of Hydrology,2015,527:747 − 753. doi: 10.1016/j.jhydrol.2015.05.038
[10] LIANG Xiuyu,ZHAN Hongbin,ZHANG Youkuan,et al. Underdamped slug tests with unsaturated-saturated flows by considering effects of wellbore skins[J]. Hydrological Processes,2018,32:968 − 980. doi: 10.1002/hyp.11471
[11] HVORSLEV M J. Time lag and soil permeability in ground-water observations[M]. Mississippi:US Army Corps of Engineers,Waterways Experiment Station Bulletin,1951.
[12] BOUWER H,RICE R C. A slug test for determining hydraulic conductivity of unconfined aquifers with completely or partially penetrating wells[J]. Water Resources Research,1976,12(3):423 − 428. doi: 10.1029/WR012i003p00423
[13] COOPER H H,BREDEHOEFT J D,PAPADOPULOS I S. Response of a finite-diameter well to an instantaneous charge of water[J]. Water Resources Research,1967,3(1):263 − 269. doi: 10.1029/WR003i001p00263
[14] BUTLER J J,ZHAN Xiaoyong. Hydraulic tests in highly permeable aquifers[J]. Water Resources Research,2004,40(12):W12402.
[15] AUDOUIN O,BODIN J. Cross-borehole slug test analysis in a fractured limestone aquifer[J]. Journal of Hydrology,2008,348(3/4):510 − 523.
[16] CARDIFF M,BARRASH W,THOMA M,et al. Information content of slug tests for estimating hydraulic properties in realistic,high-conductivity aquifer scenarios[J]. Journal of Hydrology,2011,403(1/2):66 − 82.
[17] QUINN P M,KLAMMLER H,CHERRY J A,et al. Insights from unsteady flow analysis of underdamped slug tests in fractured rock[J]. Water Resources Research,2018,54(8):5825 − 5840. doi: 10.1029/2018WR022874
[18] 文章,李旭. 考虑表皮效应的径向溶质迁移模型以及半解析解[J]. 地质科技通报,2020,39(1):60 − 66. [WEN Zhang,LI Xu. Semi-analytical solution for radial solute transport model with skin effect[J]. Bulletin of Geological Science and Technology,2020,39(1):60 − 66. (in Chinese with English abstract)]
WEN Zhang, LI Xu. Semi-analytical solution for radial solute transport model with skin effect[J]. Bulletin of Geological Science and Technology, 2020, 39(1): 60 − 66. (in Chinese with English abstract)
[19] WEN Zhang,HUANG Guanhua,ZHAN Hongbin. Non-Darcian flow to a well in a leaky aquifer using the Forchheimer equation[J]. Hydrogeology Journal,2011,19(3):563 − 572. doi: 10.1007/s10040-011-0709-2
[20] LIN Yingfan,YEH H D. A semi-analytical solution for slug test by considering near-well formation damage and nonlinear flow[J]. Water Resources Research,2022,58(3):e2021WR031368. doi: 10.1029/2021WR031368
[21] ZHANG Weishe,JIAO Yuyong,ZHANG Guohua,et al. Analysis of the mechanism of water inrush geohazards in deep-buried tunnels under the complex geological environment of karst cave-fractured zone[J]. Journal of Earth Science,2022,33(5):1204 − 1218. doi: 10.1007/s12583-022-1619-z
[22] 赵燕容,周志芳. 基于Kipp和CBP模型确定含水层渗透性的现场微水试验对比研究[J]. 工程勘察,2012,40(12):32 − 38. [ZHAO Yanrong,ZHOU Zhifang. Comparative study on field slug tests to determine aquifer permeability based on Kipp model and CBP model[J]. Geotechnical Investigation & Surveying,2012,40(12):32 − 38. (in Chinese with English abstract)]
ZHAO Yanrong, ZHOU Zhifang. Comparative study on field slug tests to determine aquifer permeability based on Kipp model and CBP model[J]. Geotechnical Investigation & Surveying, 2012, 40(12): 32 − 38. (in Chinese with English abstract)
[23] 秦宗浩. 常州微水试验在确定含水层渗透系数应用对比[J]. 山西建筑,2022,48(21):93 − 95. [QIN Zonghao. Comparison of application of slug test in determining permeability coefficient of aquifer in Changzhou[J]. Shanxi Architecture,2022,48(21):93 − 95. (in Chinese with English abstract)]
QIN Zonghao. Comparison of application of slug test in determining permeability coefficient of aquifer in Changzhou[J]. Shanxi Architecture, 2022, 48(21): 93 − 95. (in Chinese with English abstract)
[24] JR B J J. A simple correction for slug tests in small-diameter wells[J]. Ground Water,2002,40(3):303 − 307. doi: 10.1111/j.1745-6584.2002.tb02658.x
[25] DAUSSE A,GUIHÉNEUF N,PARKER B L. Impact of flow geometry on parameter uncertainties for underdamped slug tests in fractured rocks[J]. Journal of Hydrology,2021,592:125567. doi: 10.1016/j.jhydrol.2020.125567
[26] GREENE E A,SHAPIRO,A M,CARTER J M. Hydrogeologic characterization of the Minnelusa and Madison aquifers near Spearfish,South Dakota (Vol. 98)[R]. Rapid:U. S. Dept. of the Interior,U. S. Geological Survey,1999.
[27] 王全荣,唐仲华,文章,等. 越流含水层抽水井附近非达西流与达西流区界面位置变化规律研究[J]. 水利学报,2012,43(10):1171 − 1178. [WANG Quanrong,TANG Zhonghua,WEN Zhang,et al. Numeric simulation for flow to a pumping well with moving boundary of the non-Darcian flow region in a leaky aquifer[J]. Journal of Hydraulic Engineering,2012,43(10):1171 − 1178. (in Chinese with English abstract)]
WANG Quanrong, TANG Zhonghua, WEN Zhang, et al. Numeric simulation for flow to a pumping well with moving boundary of the non-Darcian flow region in a leaky aquifer[J]. Journal of Hydraulic Engineering, 2012, 43(10): 1171 − 1178. (in Chinese with English abstract)
-




 下载:
下载: